Mnemonics
Mnemonics can assist with learning the meaning of APL glyphs and where on they keyboard they are found for typing them. Both of these skills are essential for an effective APL programmer. This article provides such aide-mémoires.
Pairing glyphs with their meaning
Many glyphs have meaning identical to their mathematical counterparts.
⋄ (Diamond) separates statements. That is, no functions or operators can break through ⋄, just as diamonds are virtually indestructible.
⌺ looks like a ⋄-shaped Stencil laid on a piece of paper, ⎕.
! is Binomial in addition to Factorial, as the two are closely related.
⌶ (I-beam) calls system services. APL was originally developed at IBM, so system services were also IBM services. ⌶ is an I-beam and I-beam is pronounced almost identically to IBM.
@ applies a function or substitutes elements at specific locations.
⍋ and ⍒ give the indices (grades) needed to sort ascending and descending respectively, and look like an ascending and descending supersonic transport, respectively.
⌽, ⊖, and ⍉ reverse or transpose an array over a given axis. The ○ part of the glyphs symbolise the array, while the line component (|, \, or -) indicates the line across which the reversal/transposal is done.
⍟ looks like the cross-section of a tree log
⍱ and ⍲ (Nor and Nand) have the Not glyph ~ on top of or overlaid on the Or glyph ∨ and And glyph ∧ respectively.
× can be seen as an when monadic, indicating the unknown sign to be determined.
+ negates the imaginary part (that is, it conjugates) by analogy to monadic - which negates both the real and the imaginary parts.
÷ takes a default left argument of 1 (thus computing the reciprocal), that being the identity element of division.
⌹ is matrix divide with a ⎕ symbolising a matrix and an inscribed ÷ for "divide".
? symbolises the unknown, and thus rolls dice and deals cards randomly.
⍺ and ⍵ are the leftmost and rightmost letters of the Greek alphabet. They therefore denote the left and right arguments of dfns, respectively.
∊ is the Greek letter Epsilon which corresponds to the letter E for Enlist and Element of.
⍴ is the Greek letter Rho which corresponds to the letter R for Reshape.
~ is Not when monadic, but its dyadic form, Without, can also be remembered as but not.
⍨ is a monadic operator that looks like a face. When its derived function is applied monadically, it can be called selfie, in that it applies the operand function to the argument with the argument itself as left argument too.
↑ and ↓ (Mix and Split) increase and decrease rank (if possible) when used monadically.
↓ drops elements, and so it points down, the direction in which things are dropped. Take uses ↑ by analogy.
⍳ is the Greek letter Iota which corresponds to the letter I for Index generator and Index of.
⍸ is also the Greek letter Iota which corresponds to the letter I for Indices and Interval Index.
○ is a circle for Circular functions and the ratio between the circumference and the diameter of a circle, Pi.
⍥ and ⍤ (Over and Atop) both apply the left operand after the right operand. However, ⍥ has a larger "circle of influence" in that it applies its right operand twice (once on each argument) while ⍤ only applies it once (between the arguments).
* and ⍣ repeatedly apply multiplication and a function, respectively. The star symbolises power (function)/power (operator).
← assigns by putting the value on its right into the name on its left.
→ points at the destination it is branching to.
⍬ (Zilde) is a combination of ~ for Without and 0 indicating numbers. Indeed, it is the "vector without numbers", equivalent to 0~0.
⊣ and ⊢ point a finger towards the left and right, which are exactly the argument they, respectively, return.
⎕ is the prefix for all system names, and also manages input from the console as well as output to the console. For that, it is a stylised console. ⍞ looks like a ⎕ with a quote ' indicating string input and message output.
⌈ and ⌊ are pictograms of a wall with a piece of ceiling and floor, respectively.
⌈ and ⌊ can also be seen as indicators on a vertical number line, pointing at the maximum and minimum, respectively.
∇ is an upside-down Greek Delta, which corresponds to the letter D for Defined function or (own) definition (for recursion).
⌸ (Key) applies a function for each collection of all elements that are equal (⌸).
≡ can be see as a stack of layers. When used monadically, it finds the depth of an array.
≢ looks like a tally mark. It being sideways can be justified by it counting the length of the leading axis; the vertical axis of a matrix.
⊂ encloses its argument in a layer of nesting, and Disclose uses ⊃ by analogy. ⊆ is exactly like ⊂ except that it only does a conditional enclose, namely only if the argument is simple.
⊂ and ⊆ enclose at specific locations, per a specification, so their dyadic forms are Partitioned enclose and Partition, respectively.
∪ is a styled letter U for Unique or Union if used dyadically.
⊥ looks like the base of a pillar, converting from that base. Antibase uses ⊤ by analogy, and looks a styled letter T for "To base". ⊤ and ⊥ are also respectively known as Encode and Decode. To remember which is which, ⊤ looks like a styled letter T, so think "Ten-code".
⍝ looks like a filament lamp and provides enlightenment by indicating comments.
, concatenates arrays, much like the common punctuation symbol concatenates phrases. ⍪ has an added styled row, indicating that for matrices, it concatenates additional rows.
. is just a low dot, but performs the same operation (though generalised) as traditional mathematics' dot product.
/ and ⌿ are also called "by" which can be remembered as reduce by.
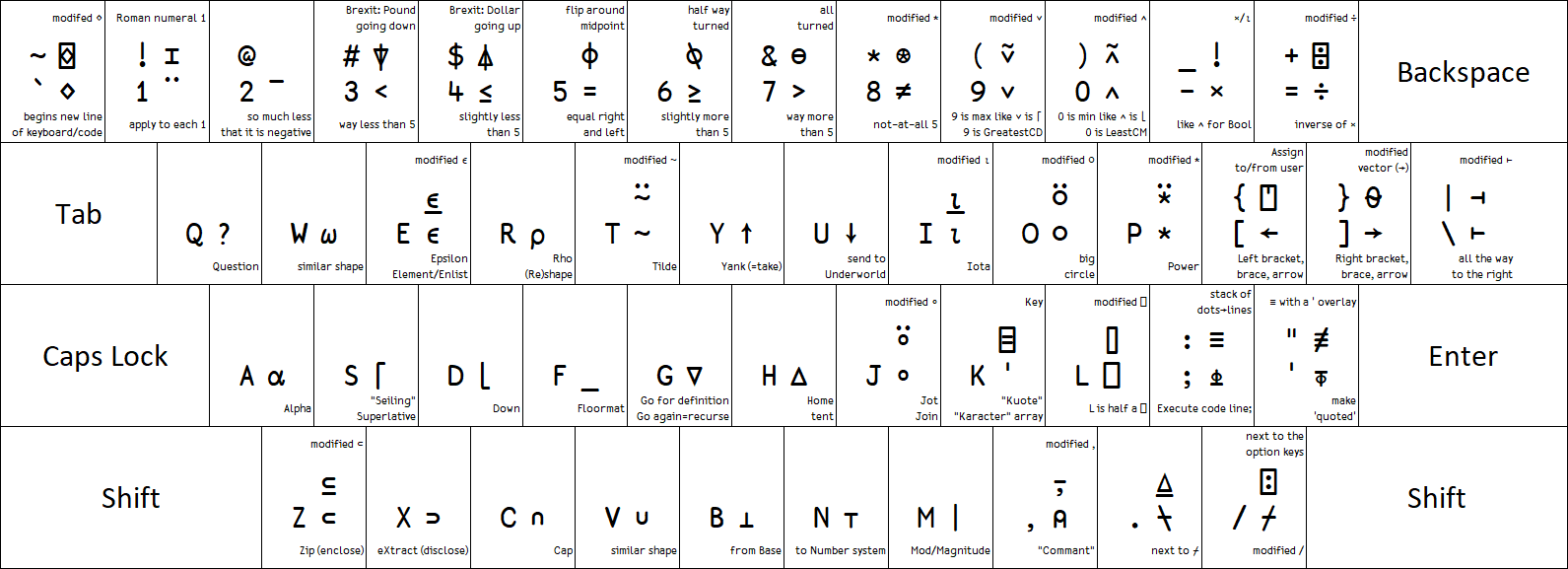
Pairing glyphs/functionality with their keyboard locations
The following mnemonics are for Dyalog APL's US English keyboard layout, but can easily be adapted to similar layouts.
Number row keys
⋄ begins new APL expressions just like ` button begins the main section of the keyboard. ⌺ is a modified version of ⌺, so it is Shift+⋄.
¨ applies a function to each 1 of the argument elements, so it is on APL+1. ⌶ looks like a Roman numeral 1, so it also lives on the 1, albeit in the shifted position.
¯, <, ≤, =, ≥, >, and ≠ form a block. The number line 1–9 (because 0 on the far right) is split into two equal halves by 5 so that gives =. 4 and 6 are slightly less and more, respectively, so they give ≤ and ≥. 3 and 7 are much less and more, respectively, so they give < and >. Finally, 2 is so much less that it is negative, giving the negative sign ¯, and 8 is so much greater that it is completely unequal, ≠.
⍒ and ⍋ are located on # (read "pound", £ on British keyboards). ⍒ pointing down is on the lower of the two numbers 3 and 4. This can be remembered as the pound going down due to Brexit.
⌽ mirrors an array over its vertical centre, so it is placed on the centre of the 1–9 number line. ⍉ is slightly off centre, while ⊖ has completely fallen over.
∨ and ∧ are on the largest (9) and smallest (0) digits, respectively, as ∨ is inclusive (any argument being true gives true) while ∧ is exclusive (any false gives false). Their negated versions ⍱ and ⍲ are on the shifted positions.
× is adjacent to ∧ for which it is equivalent on Boolean arguments. ! is above it, being ×/⍳. ÷ is adjacent to its inverse, ×. And ⌹ is in the shifted position, being the matrix equivalent of ÷.
Top row keys
? is on q for question.
⍵, ∊, and ⍳ look similar to w, e, and i. ⍷ and ⍸ are the shifted variants of ∊ and ⍳. The Greek letters ∊, and ⍳ are also equivalent to the Latin e, and i.
⍴ is the Greek equivalent of r.
~ is on t for its name tilde, and its variant with diaeresis, ⍨, is on the shifted position.
↑ is on y for yank (=take), and ↓ is on the adjacent u for drop down under.
○ is on o due to the similar looks, and ⍥ is the shifted variant. ⍥ is also on O for Over.
* is on p for power, and ⍣ is the shifted variant.
← and → match the directionality of [ and ]. ⍞ is usually immediately assigned to/from using ←, so they share key. ⍬ is the empty vector and vectors are usually pictured as arrows pointing right, so it shares key with →.
⊢ is on the rightmost key, and its shifted variant ⊣ points the other way.
Home row keys
⍺ looks similar to a. The Greek letter ⍺is also equivalent to the Latin a. Finally, ⍺, being the left argument, is (below and) to the left of the right argument ⍵ on w.
⌈ is on s for seiling (since c is pronounced like s here) and also finds the superlative argument. ⌊ is adjacent on d for rounding down.
_ is on f for being a floormat.
∇ is on g for go!, indicating the beginning of a function definition or going around again (recursion). Adjecent, we find its upturned variant, ∆, which is a home tent, located on on h.
∘ on j is called jot. Its variant with diaeresis, ⍤, is on the shifted position.
' is on k for kuote (since q is reserved for question, as in "Q&A").
⌸ is also on K for Key.
⎕ is on L which looks like its lower left half. ⌷ is its squished equivalent, on the shifted key.
⍎ executes code, and is on ; which is a ubiquitous symbol in code. Adjacent is ⍕ which is its inverse and is found on ' because it makes things into text, as indicated by the quote.
≡ is on : — a stack of lines on a stack of dots. ≢ is its negation and is found adjacent to it, on the ' key, ≢ being a ≡ with a ' drawn on top.
Bottom row keys
⊂ is on z because it zips up (encloses) a value into a scalar. Its shifted variant ⊆ only does so conditionally. Its inverse and mirror-image, ⊃, is located adjacent, on x because it extracts (discloses) the content of an enclosed scalar.
∩ is on c for cap, and its upturned variant, ∪, is adjacent on v to which it is visually similar.
⊥ is on b because it evaluates digits in a given base. Its upturned variant ⊤ is adjacent on n because it (e)ncodes a normal number to a custom number system.
| is on m for modulo/magnitude and modulus.
⍝ is on , due to the similarity of the words comma and comment. Shifted , gives the barred version, ⍪.
⍀ is adjacent to its mirrored counter-part ⌿ which in turn is a barred version of its key, /.
⍠ varies the meaning of its operand, so it is in the corner on ?, adjacent to all the shifting keys.
Summary
All the above mnemonics are annotated on the below image of a US English keyboard layout:
Pairing monadic and dyadic meanings
Meaning pairings fall into three groups as follows.
Monadic form is like dyadic form with a default left argument
| Glyph | Default left argument |
|---|---|
+
|
0J¯2×11○x i.e.
|
-
|
0 |
×
|
÷(|x)+x=0 i.e.
|
÷
|
1 |
*
|
*1 i.e.
|
⍟
|
*1 i.e.
|
,
|
⍬ (for scalars and vectors only)
|
?
|
1 (almost; monadic form gives a scalar, dyadic form gives a vector) |
⍒
|
⎕UCS 0,⍳111411
|
⍋
|
⎕UCS 0,⍳111411
|
⍉
|
⌽⍳≢⍴x
|
⍎
|
⎕THIS
|
⌹
|
∘.=⍨⍳≢x i.e.
|
⊂
|
,1 (almost; monadic form gives a scalar, dyadic form gives a vector)
|
⊃
|
⊂(≢⍴x)⍴1
|
∪
|
∪x
|
⌷
|
⊂⍳≢⌷x
|
⊣
|
x
|
⊢
|
x
|
Both forms are good fit for the glyph
| Glyph | Explanation |
|---|---|
≡
|
indicates (3) layers of depth for the monadic form |
≢
|
indicates a counting rod marking for the monadic form |
↑
|
take elements and increase rank |
↓
|
drop elements and decrease rank |
∊
|
"element of" and "enlist" |
⊆
|
"enclose at positions where condition is met" and "enclose on condition of being simple" |
⍸
|
"indices where elements fit into intervals" and "indices where true" |
⍪
|
,[1]x (for non-scalars) and ,⍤¯1 (for higher-rank arrays)
|
| Glyph | Relationship |
|---|---|
⌈
|
next higher integer or highest argument |
⌊
|
next lower integer or lowest argument |
|
|
both forms can be called modulo and use the symbol: and |
!
|
factorial is prominent in the formula for binomial |
○
|
both the trigonometric functions and relate to the (unit) circle |
~
|
"not" and "but not" |
≠
|
monadic means "not equal to any preceding item" |
⍴
|
shape and reshape |
⍳
|
indices of and index of |
⌽
|
rotate and mirror along last axis |
⊖
|
rotate and mirror along first axis |
⍕
|
format and format with specification |
| APL development [edit] | |
|---|---|
| Interface | Session ∙ Typing glyphs (on Linux) ∙ Fonts ∙ Text editors |
| Publications | Introductions ∙ Learning resources ∙ Simple examples ∙ Advanced examples ∙ Mnemonics ∙ ISO 8485:1989 ∙ ISO/IEC 13751:2001 ∙ A Dictionary of APL ∙ Case studies ∙ Documentation suites ∙ Books ∙ Papers ∙ Videos ∙ APL Quote Quad ∙ Vector journal ∙ Terminology (Chinese, German) ∙ Neural networks ∙ Error trapping with Dyalog APL (in forms) |
| Sharing code | Backwards compatibility ∙ APLcart ∙ APLTree ∙ APL-Cation ∙ Dfns workspace ∙ Tatin ∙ Cider |
| Implementation | Resources ∙ Open-source ∙ Magic function ∙ Performance ∙ APL hardware |
| Developers | Timeline of corporations ∙ APL2000 ∙ Dyalog ∙ IBM ∙ IPSA ∙ STSC |
| APL glyphs [edit] | |
|---|---|
| Information | Glyph ∙ Typing glyphs (on Linux) ∙ Unicode ∙ Fonts ∙ Mnemonics ∙ Overstrikes ∙ Migration level |
| Individual glyphs | Jot (∘) ∙ Right Shoe (⊃) ∙ Up Arrow (↑) ∙ Zilde (⍬) ∙ High minus (¯) ∙ Dot (.) ∙ Del (∇)
|







![{\displaystyle {\frac {1}{|x|+[x=0]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cad7858dc53eb43a810914c95f90fbba8f9caad6)




