Simple examples: Difference between revisions
m (Text replacement - "<source" to "<syntaxhighlight") |
m (→Parenthesis nesting level: Link "one-liner") |
||
| (One intermediate revision by one other user not shown) | |||
| Line 6: | Line 6: | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
{(+⌿⍵)÷≢⍵} | {(+⌿⍵)÷≢⍵} | ||
</ | </syntaxhighlight> | ||
It is unnamed: the enclosing braces mark it as a function definition. It can be assigned a name for use later, or used anonymously in a more complex expression. | It is unnamed: the enclosing braces mark it as a function definition. It can be assigned a name for use later, or used anonymously in a more complex expression. | ||
The <syntaxhighlight lang=apl inline>⍵</ | The <syntaxhighlight lang=apl inline>⍵</syntaxhighlight> refers to the argument of the function, a list (or 1-dimensional array) of numbers. The <syntaxhighlight lang=apl inline>≢</syntaxhighlight> denotes the [[tally]] function, which returns here the length of (number of elements in) the argument <syntaxhighlight lang=apl inline>⍵</syntaxhighlight>. The divide symbol <syntaxhighlight lang=apl inline>÷</syntaxhighlight> has its usual meaning. | ||
The parenthesised <syntaxhighlight lang=apl inline>+⌿⍵</ | The parenthesised <syntaxhighlight lang=apl inline>+⌿⍵</syntaxhighlight> denotes the sum of all the elements of <syntaxhighlight lang=apl inline>⍵</syntaxhighlight>. The <syntaxhighlight lang=apl inline>⌿</syntaxhighlight> operator combines with the <syntaxhighlight lang=apl inline>+</syntaxhighlight> function: the <syntaxhighlight lang=apl inline>⌿</syntaxhighlight> fixes the <syntaxhighlight lang=apl inline>+</syntaxhighlight> function between each element of <syntaxhighlight lang=apl inline>⍵</syntaxhighlight>, so that | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
+⌿ 1 2 3 4 5 6 | +⌿ 1 2 3 4 5 6 | ||
21 | 21 | ||
</ | </syntaxhighlight> | ||
is the same as | is the same as | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
1+2+3+4+5+6 | 1+2+3+4+5+6 | ||
21 | 21 | ||
</ | </syntaxhighlight> | ||
=== Operators === | === Operators === | ||
[[Operator]]s like <syntaxhighlight lang=apl inline>⌿</ | [[Operator]]s like <syntaxhighlight lang=apl inline>⌿</syntaxhighlight> can be used to derive new functions not only from [[primitive function]]s like <syntaxhighlight lang=apl inline>+</syntaxhighlight>, but also from defined functions. For example | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
{⍺,', ',⍵}⌿ | {⍺,', ',⍵}⌿ | ||
</ | </syntaxhighlight> | ||
will transform a list of strings representing words into a comma-separated list: | will transform a list of strings representing words into a comma-separated list: | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
| Line 32: | Line 32: | ||
│cow, sheep, cat, dog│ | │cow, sheep, cat, dog│ | ||
└────────────────────┘ | └────────────────────┘ | ||
</ | </syntaxhighlight> | ||
So back to our mean example. <syntaxhighlight lang=apl inline>(+⌿⍵)</ | So back to our mean example. <syntaxhighlight lang=apl inline>(+⌿⍵)</syntaxhighlight> gives the sum of the list, which is then divided by <syntaxhighlight lang=apl inline>≢⍵</syntaxhighlight>, the number elements in it. | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
{(+⌿⍵)÷≢⍵} 3 4.5 7 21 | {(+⌿⍵)÷≢⍵} 3 4.5 7 21 | ||
8.875 | 8.875 | ||
</ | </syntaxhighlight> | ||
=== Tacit programming === | === Tacit programming === | ||
| Line 47: | Line 47: | ||
(+⌿÷≢) 3 4.5 7 21 | (+⌿÷≢) 3 4.5 7 21 | ||
8.875 | 8.875 | ||
</ | </syntaxhighlight> | ||
This is a so called 3-train, also known as a ''fork''. It is evaluated like this: | This is a so called 3-train, also known as a ''fork''. It is evaluated like this: | ||
{| | {| | ||
|<syntaxhighlight lang=apl>(+⌿ ÷ ≢) 3 4.5 7 21</ | |<syntaxhighlight lang=apl>(+⌿ ÷ ≢) 3 4.5 7 21</syntaxhighlight>|| {{←→}} ||<syntaxhighlight lang=apl>(+⌿ 3 4.5 7 21) ÷ (≢ 3 4.5 7 21)</syntaxhighlight> | ||
|} | |} | ||
Note that <syntaxhighlight lang=apl inline>+⌿</ | Note that <syntaxhighlight lang=apl inline>+⌿</syntaxhighlight> is evaluated as a single derived function. | ||
The general scheme for monadic 3-trains is the following: | The general scheme for monadic 3-trains is the following: | ||
{| | {| | ||
|<syntaxhighlight lang=apl>(f g h) ⍵</ | |<syntaxhighlight lang=apl>(f g h) ⍵</syntaxhighlight>|| {{←→}} ||<syntaxhighlight lang=apl>(f ⍵) g (h ⍵)</syntaxhighlight> | ||
|} | |} | ||
| Line 65: | Line 65: | ||
APL represents text as character lists (vectors), making many text operations trivial. | APL represents text as character lists (vectors), making many text operations trivial. | ||
=== Split text by delimiter === | === Split text by delimiter === | ||
<syntaxhighlight lang=apl inline>≠</ | <syntaxhighlight lang=apl inline>≠</syntaxhighlight> gives 1 for true and 0 for false. It [[scalar function|pairs up]] a single element argument with all the elements of the other arguments: | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
','≠'comma,delimited,text' | ','≠'comma,delimited,text' | ||
1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 | 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 | ||
</ | </syntaxhighlight> | ||
<syntaxhighlight lang=apl inline>⊢</ | <syntaxhighlight lang=apl inline>⊢</syntaxhighlight> returns its right argument: | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
','⊢'comma,delimited,text' | ','⊢'comma,delimited,text' | ||
comma,delimited,text | comma,delimited,text | ||
</ | </syntaxhighlight> | ||
<syntaxhighlight lang=apl inline>⊆</ | <syntaxhighlight lang=apl inline>⊆</syntaxhighlight> returns a list of runs as indicated by runs of 1s, leaving out elements indicated by 0s: | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
1 1 0 1 1 1⊆'Hello!' | 1 1 0 1 1 1⊆'Hello!' | ||
| Line 81: | Line 81: | ||
│He│lo!│ | │He│lo!│ | ||
└──┴───┘ | └──┴───┘ | ||
</ | </syntaxhighlight> | ||
We use the comparison [[vector]] to [[partition]] the right argument: | We use the comparison [[vector]] to [[partition]] the right argument: | ||
| Line 90: | Line 90: | ||
│comma│delimited│text│ | │comma│delimited│text│ | ||
└─────┴─────────┴────┘ | └─────┴─────────┴────┘ | ||
</ | </syntaxhighlight> | ||
{{Works in|[[Dyalog APL]]}} | {{Works in|[[Dyalog APL]]}} | ||
Notice that you can read the [[tacit]] function <syntaxhighlight lang=apl inline>≠⊆⊢</ | Notice that you can read the [[tacit]] function <syntaxhighlight lang=apl inline>≠⊆⊢</syntaxhighlight> like an English sentence: ''The inequality partitions the right argument''. | ||
Many dialects do not support the above [[tacit]] syntax, and use the [[glyph]] <syntaxhighlight lang=apl inline>⊂</ | Many dialects do not support the above [[tacit]] syntax, and use the [[glyph]] <syntaxhighlight lang=apl inline>⊂</syntaxhighlight> for partition [[primitive function]]. In such dialects, the following formulation can be used: | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
(','≠s)⊂s←'comma,delimited,text' | (','≠s)⊂s←'comma,delimited,text' | ||
</ | </syntaxhighlight> | ||
{{Works in|[[APL2]], [[APLX]], [[GNU APL]]}} | {{Works in|[[APL2]], [[APLX]], [[GNU APL]]}} | ||
This assigns the text to the variable <syntaxhighlight lang=apl inline>s</ | This assigns the text to the variable <syntaxhighlight lang=apl inline>s</syntaxhighlight>, then separately computes the partitioning vector and applies it. | ||
=== Indices of multiple elements === | === Indices of multiple elements === | ||
<syntaxhighlight lang=apl inline>∊</ | <syntaxhighlight lang=apl inline>∊</syntaxhighlight> gives us a mask for elements (characters) in the left argument that are members of the right argument: | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
'mississippi'∊'sp' | 'mississippi'∊'sp' | ||
0 0 1 1 0 1 1 0 1 1 0 | 0 0 1 1 0 1 1 0 1 1 0 | ||
</ | </syntaxhighlight> | ||
<syntaxhighlight lang=apl inline>⍸</ | <syntaxhighlight lang=apl inline>⍸</syntaxhighlight> gives us the indices where true (1): | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
⍸'mississippi'∊'sp' | ⍸'mississippi'∊'sp' | ||
3 4 6 7 9 10 | 3 4 6 7 9 10 | ||
</ | </syntaxhighlight> | ||
We can combine this into an anonymous infix (dyadic) function: | We can combine this into an anonymous infix (dyadic) function: | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
'mississippi' (⍸∊) 'sp' | 'mississippi' (⍸∊) 'sp' | ||
3 4 6 7 9 10 | 3 4 6 7 9 10 | ||
</ | </syntaxhighlight> | ||
{{Works in|[[Dyalog APL]], [[NARS2000]], [[dzaima/APL]]}} | {{Works in|[[Dyalog APL]], [[NARS2000]], [[dzaima/APL]]}} | ||
| Line 127: | Line 127: | ||
1 0 0 0 0 0 0 | 1 0 0 0 0 0 0 | ||
0 0 0 0 0 0 0 | 0 0 0 0 0 0 0 | ||
</ | </syntaxhighlight> | ||
Then it is simply a matter of performing a sum-reduce <syntaxhighlight lang=apl inline>+/</ | Then it is simply a matter of performing a sum-reduce <syntaxhighlight lang=apl inline>+/</syntaxhighlight> to calculate the total frequency of each character:<ref name="Marshall LambaConf 2019">[[Marshall Lochbaum]] used this example as part of his talk on [[Outer Product]] at LambdaConf 2019.</ref> | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
+/ 'abcd' ∘.= 'cabbage' | +/ 'abcd' ∘.= 'cabbage' | ||
2 2 1 0 | 2 2 1 0 | ||
</ | </syntaxhighlight> | ||
=== Parenthesis nesting level === | === Parenthesis nesting level === | ||
{{quote | "Ken was showing some slides — and one of his slides had something on it that I was later to learn was an APL one-liner. And he tossed this off as an example of the expressiveness of the APL notation. I believe the one-liner was one of the standard ones for indicating the nesting level of the parentheses in an algebraic expression. But the one-liner was very short — ten characters, something like that — and having been involved with programming things like that for a long time and realizing that it took a reasonable amount of code to do, I looked at it and said, “My God, there must be something in this language.”"|[[Alan Perlis]]. ''[https://www.jsoftware.com/papers/perlis78.htm Almost Perfect Artifacts Improve only in Small Ways: APL is more French than English]'' at [[APL78]].}} | {{quote | "Ken was showing some slides — and one of his slides had something on it that I was later to learn was an APL [[one-liner]]. And he tossed this off as an example of the expressiveness of the APL notation. I believe the one-liner was one of the standard ones for indicating the nesting level of the parentheses in an algebraic expression. But the one-liner was very short — ten characters, something like that — and having been involved with programming things like that for a long time and realizing that it took a reasonable amount of code to do, I looked at it and said, “My God, there must be something in this language.”"|[[Alan Perlis]]. ''[https://www.jsoftware.com/papers/perlis78.htm Almost Perfect Artifacts Improve only in Small Ways: APL is more French than English]'' at [[APL78]].}} | ||
What was the one-liner for the nesting level of parentheses? It would take a bit of work to figure out, because at the time of the meeting Perlis described, no APL implementation existed. Two possibilities are explained here. | What was the one-liner for the nesting level of parentheses? It would take a bit of work to figure out, because at the time of the meeting Perlis described, no APL implementation existed. Two possibilities are explained here. | ||
==== Method A ==== | ==== Method A ==== | ||
For this more complex computation, we can expand on the previous example's use of <syntaxhighlight lang=apl inline>∘.=</ | For this more complex computation, we can expand on the previous example's use of <syntaxhighlight lang=apl inline>∘.=</syntaxhighlight>. First we compare all characters to the opening and closing characters; | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
'()'∘.='plus(square(a),plus(square(b),times(2,plus(a,b)))' | '()'∘.='plus(square(a),plus(square(b),times(2,plus(a,b)))' | ||
0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 | 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 | ||
0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 | 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 | ||
</ | </syntaxhighlight> | ||
An opening increases the current level, while a closing decreases, so we convert this to ''changes'' (or ''deltas'') by subtracting the bottom row from the top row: | An opening increases the current level, while a closing decreases, so we convert this to ''changes'' (or ''deltas'') by subtracting the bottom row from the top row: | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
-⌿'()'∘.='plus(square(a),plus(square(b),times(2,plus(a,b)))' | -⌿'()'∘.='plus(square(a),plus(square(b),times(2,plus(a,b)))' | ||
0 0 0 0 1 0 0 0 0 0 0 1 0 ¯1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 ¯1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 ¯1 ¯1 ¯1 | 0 0 0 0 1 0 0 0 0 0 0 1 0 ¯1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 ¯1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 ¯1 ¯1 ¯1 | ||
</ | </syntaxhighlight> | ||
The running sum is what we're looking for: | The running sum is what we're looking for: | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
+\-⌿'()'∘.='plus(square(a),plus(square(b),times(2,plus(a,b)))' | +\-⌿'()'∘.='plus(square(a),plus(square(b),times(2,plus(a,b)))' | ||
0 0 0 0 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 2 2 2 2 2 2 2 3 3 2 2 2 2 2 2 2 3 3 3 3 3 3 3 4 4 4 4 3 2 1 | 0 0 0 0 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 2 2 2 2 2 2 2 3 3 2 2 2 2 2 2 2 3 3 3 3 3 3 3 4 4 4 4 3 2 1 | ||
</ | </syntaxhighlight> | ||
{{Works in|all APLs}} | {{Works in|all APLs}} | ||
==== Method B ==== | ==== Method B ==== | ||
Alternatively, we can utilise that if the [[Index Of]] function <syntaxhighlight lang=apl inline>⍳</ | Alternatively, we can utilise that if the [[Index Of]] function <syntaxhighlight lang=apl inline>⍳</syntaxhighlight> doesn't find what it is looking for, it returns the next index after the last element in the the lookup array: | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
'ABBA'⍳'ABC' | 'ABBA'⍳'ABC' | ||
| Line 162: | Line 162: | ||
'()'⍳'plus(square(a),plus(square(b),times(2,plus(a,b)))' | '()'⍳'plus(square(a),plus(square(b),times(2,plus(a,b)))' | ||
3 3 3 3 1 3 3 3 3 3 3 1 3 2 3 3 3 3 3 1 3 3 3 3 3 3 1 3 2 3 3 3 3 3 3 1 3 3 3 3 3 3 1 3 3 3 2 2 2 | 3 3 3 3 1 3 3 3 3 3 3 1 3 2 3 3 3 3 3 1 3 3 3 3 3 3 1 3 2 3 3 3 3 3 3 1 3 3 3 3 3 3 1 3 3 3 2 2 2 | ||
</ | </syntaxhighlight> | ||
Whenever we have a 1 the parenthesis level increases, and when we have a 2 it decreases. If we have a 3, it remains as-is. We can do this mapping by indexing into these values: | Whenever we have a 1 the parenthesis level increases, and when we have a 2 it decreases. If we have a 3, it remains as-is. We can do this mapping by indexing into these values: | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
1 ¯1 0['()'⍳'plus(square(a),plus(square(b),times(2,plus(a,b)))'] | 1 ¯1 0['()'⍳'plus(square(a),plus(square(b),times(2,plus(a,b)))'] | ||
0 0 0 0 1 0 0 0 0 0 0 1 0 ¯1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 ¯1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 ¯1 ¯1 ¯1 | 0 0 0 0 1 0 0 0 0 0 0 1 0 ¯1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 ¯1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 ¯1 ¯1 ¯1 | ||
</ | </syntaxhighlight> | ||
The running sum is what we're looking for: | The running sum is what we're looking for: | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
+\1 ¯1 0['()'⍳'plus(square(a),plus(square(b),times(2,plus(a,b)))'] | +\1 ¯1 0['()'⍳'plus(square(a),plus(square(b),times(2,plus(a,b)))'] | ||
0 0 0 0 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 2 2 2 2 2 2 2 3 3 2 2 2 2 2 2 2 3 3 3 3 3 3 3 4 4 4 4 3 2 1 | 0 0 0 0 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 2 2 2 2 2 2 2 3 3 2 2 2 2 2 2 2 3 3 3 3 3 3 3 4 4 4 4 3 2 1 | ||
</ | </syntaxhighlight> | ||
{{Works in|all APLs}} | {{Works in|all APLs}} | ||
| Line 189: | Line 189: | ||
│MPLFF│⌺ ⌺⌺│ | │MPLFF│⌺ ⌺⌺│ | ||
└─────┴─────┘ | └─────┴─────┘ | ||
</ | </syntaxhighlight> | ||
</p> | </p> | ||
Retrieve elements of the grid where there are spaces in the grille. | Retrieve elements of the grid where there are spaces in the grille. | ||
| Line 195: | Line 195: | ||
grid[⍸grille=' '] | grid[⍸grille=' '] | ||
ILIKEAPL | ILIKEAPL | ||
</ | </syntaxhighlight> | ||
An alternative method using [[ravel]]. | An alternative method using [[ravel]]. | ||
<syntaxhighlight lang=apl> | <syntaxhighlight lang=apl> | ||
(' '=,grille)/,grid | (' '=,grille)/,grid | ||
ILIKEAPL | ILIKEAPL | ||
</ | </syntaxhighlight> | ||
===References=== | ===References=== | ||
<references/> | <references/> | ||
Latest revision as of 01:32, 10 March 2024
This page contains examples that show APL's strengths. The examples require minimal background and have no special dependencies. If these examples are too simple for you, have a look at our advanced examples.
Arithmetic mean
Here is an APL program to calculate the average (arithmetic mean) of a list of numbers, written as a dfn:
{(+⌿⍵)÷≢⍵}
It is unnamed: the enclosing braces mark it as a function definition. It can be assigned a name for use later, or used anonymously in a more complex expression.
The ⍵ refers to the argument of the function, a list (or 1-dimensional array) of numbers. The ≢ denotes the tally function, which returns here the length of (number of elements in) the argument ⍵. The divide symbol ÷ has its usual meaning.
The parenthesised +⌿⍵ denotes the sum of all the elements of ⍵. The ⌿ operator combines with the + function: the ⌿ fixes the + function between each element of ⍵, so that
+⌿ 1 2 3 4 5 6 21
is the same as
1+2+3+4+5+6 21
Operators
Operators like ⌿ can be used to derive new functions not only from primitive functions like +, but also from defined functions. For example
{⍺,', ',⍵}⌿
will transform a list of strings representing words into a comma-separated list:
{⍺,', ',⍵}⌿'cow' 'sheep' 'cat' 'dog'
┌────────────────────┐
│cow, sheep, cat, dog│
└────────────────────┘
So back to our mean example. (+⌿⍵) gives the sum of the list, which is then divided by ≢⍵, the number elements in it.
{(+⌿⍵)÷≢⍵} 3 4.5 7 21
8.875
Tacit programming
- Main article: Tacit programming
In APL’s tacit definition, no braces are needed to mark the definition of a function: primitive functions just combine in a way that enables us to omit any reference to the function arguments — hence tacit. Here is the same calculation written tacitly:
(+⌿÷≢) 3 4.5 7 21 8.875
This is a so called 3-train, also known as a fork. It is evaluated like this:
(+⌿ ÷ ≢) 3 4.5 7 21 |
(+⌿ 3 4.5 7 21) ÷ (≢ 3 4.5 7 21) |
Note that +⌿ is evaluated as a single derived function.
The general scheme for monadic 3-trains is the following:
(f g h) ⍵ |
(f ⍵) g (h ⍵) |
But other types of trains are also possible.
Text processing
APL represents text as character lists (vectors), making many text operations trivial.
Split text by delimiter
≠ gives 1 for true and 0 for false. It pairs up a single element argument with all the elements of the other arguments:
','≠'comma,delimited,text' 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1
⊢ returns its right argument:
','⊢'comma,delimited,text' comma,delimited,text
⊆ returns a list of runs as indicated by runs of 1s, leaving out elements indicated by 0s:
1 1 0 1 1 1⊆'Hello!' ┌──┬───┐ │He│lo!│ └──┴───┘
We use the comparison vector to partition the right argument:
','(≠⊆⊢)'comma,delimited,text' ┌─────┬─────────┬────┐ │comma│delimited│text│ └─────┴─────────┴────┘
Notice that you can read the tacit function ≠⊆⊢ like an English sentence: The inequality partitions the right argument.
Many dialects do not support the above tacit syntax, and use the glyph ⊂ for partition primitive function. In such dialects, the following formulation can be used:
(','≠s)⊂s←'comma,delimited,text'
This assigns the text to the variable s, then separately computes the partitioning vector and applies it.
Indices of multiple elements
∊ gives us a mask for elements (characters) in the left argument that are members of the right argument:
'mississippi'∊'sp' 0 0 1 1 0 1 1 0 1 1 0
⍸ gives us the indices where true (1):
⍸'mississippi'∊'sp' 3 4 6 7 9 10
We can combine this into an anonymous infix (dyadic) function:
'mississippi' (⍸∊) 'sp' 3 4 6 7 9 10
Frequency of characters in a string
The Outer Product allows for an intuitive way to compute the occurrence of characters at a given location in a string:
'abcd' ∘.= 'cabbage' 0 1 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
Then it is simply a matter of performing a sum-reduce +/ to calculate the total frequency of each character:[1]
+/ 'abcd' ∘.= 'cabbage' 2 2 1 0
Parenthesis nesting level
"Ken was showing some slides — and one of his slides had something on it that I was later to learn was an APL one-liner. And he tossed this off as an example of the expressiveness of the APL notation. I believe the one-liner was one of the standard ones for indicating the nesting level of the parentheses in an algebraic expression. But the one-liner was very short — ten characters, something like that — and having been involved with programming things like that for a long time and realizing that it took a reasonable amount of code to do, I looked at it and said, “My God, there must be something in this language.”"
Alan Perlis. Almost Perfect Artifacts Improve only in Small Ways: APL is more French than English at APL78.
What was the one-liner for the nesting level of parentheses? It would take a bit of work to figure out, because at the time of the meeting Perlis described, no APL implementation existed. Two possibilities are explained here.
Method A
For this more complex computation, we can expand on the previous example's use of ∘.=. First we compare all characters to the opening and closing characters;
'()'∘.='plus(square(a),plus(square(b),times(2,plus(a,b)))' 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1
An opening increases the current level, while a closing decreases, so we convert this to changes (or deltas) by subtracting the bottom row from the top row:
-⌿'()'∘.='plus(square(a),plus(square(b),times(2,plus(a,b)))' 0 0 0 0 1 0 0 0 0 0 0 1 0 ¯1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 ¯1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 ¯1 ¯1 ¯1
The running sum is what we're looking for:
+\-⌿'()'∘.='plus(square(a),plus(square(b),times(2,plus(a,b)))' 0 0 0 0 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 2 2 2 2 2 2 2 3 3 2 2 2 2 2 2 2 3 3 3 3 3 3 3 4 4 4 4 3 2 1
Method B
Alternatively, we can utilise that if the Index Of function ⍳ doesn't find what it is looking for, it returns the next index after the last element in the the lookup array:
'ABBA'⍳'ABC'
1 2 5
'()'⍳'plus(square(a),plus(square(b),times(2,plus(a,b)))'
3 3 3 3 1 3 3 3 3 3 3 1 3 2 3 3 3 3 3 1 3 3 3 3 3 3 1 3 2 3 3 3 3 3 3 1 3 3 3 3 3 3 1 3 3 3 2 2 2
Whenever we have a 1 the parenthesis level increases, and when we have a 2 it decreases. If we have a 3, it remains as-is. We can do this mapping by indexing into these values:
1 ¯1 0['()'⍳'plus(square(a),plus(square(b),times(2,plus(a,b)))'] 0 0 0 0 1 0 0 0 0 0 0 1 0 ¯1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 ¯1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 ¯1 ¯1 ¯1
The running sum is what we're looking for:
+\1 ¯1 0['()'⍳'plus(square(a),plus(square(b),times(2,plus(a,b)))'] 0 0 0 0 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 2 2 2 2 2 2 2 3 3 2 2 2 2 2 2 2 3 3 3 3 3 3 3 4 4 4 4 3 2 1
Grille cypher
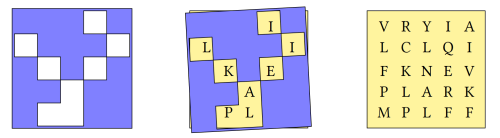
A grille is a 500 year old method for encrypting messages.
Represent both the grid of letters and the grille as character matrices.
⎕←(grid grille)←5 5∘⍴¨'VRYIALCLQIFKNEVPLARKMPLFF' '⌺⌺⌺ ⌺ ⌺⌺⌺ ⌺ ⌺ ⌺⌺⌺ ⌺⌺⌺ ⌺⌺' ┌─────┬─────┐ │VRYIA│⌺⌺⌺ ⌺│ │LCLQI│ ⌺⌺⌺ │ │FKNEV│⌺ ⌺ ⌺│ │PLARK│⌺⌺ ⌺⌺│ │MPLFF│⌺ ⌺⌺│ └─────┴─────┘
Retrieve elements of the grid where there are spaces in the grille.
grid[⍸grille=' '] ILIKEAPL
An alternative method using ravel.
(' '=,grille)/,grid
ILIKEAPL
References
- ↑ Marshall Lochbaum used this example as part of his talk on Outer Product at LambdaConf 2019.
| APL development [edit] | |
|---|---|
| Interface | Session ∙ Typing glyphs (on Linux) ∙ Fonts ∙ Text editors |
| Publications | Introductions ∙ Learning resources ∙ Simple examples ∙ Advanced examples ∙ Mnemonics ∙ ISO 8485:1989 ∙ ISO/IEC 13751:2001 ∙ A Dictionary of APL ∙ Case studies ∙ Documentation suites ∙ Books ∙ Papers ∙ Videos ∙ APL Quote Quad ∙ Vector journal ∙ Terminology (Chinese, German) ∙ Neural networks ∙ Error trapping with Dyalog APL (in forms) |
| Sharing code | Backwards compatibility ∙ APLcart ∙ APLTree ∙ APL-Cation ∙ Dfns workspace ∙ Tatin ∙ Cider |
| Implementation | Resources ∙ Open-source ∙ Magic function ∙ Performance ∙ APL hardware |
| Developers | Timeline of corporations ∙ APL2000 ∙ Dyalog ∙ IBM ∙ IPSA ∙ STSC |