Simple examples
This page contains examples that show APL's strengths. The examples require minimal background and have no special dependencies. If these examples are too simple for you, have a look at our advanced examples.
Arithmetic mean
Here is an APL program to calculate the average (arithmetic mean) of a list of numbers, written as a dfn:
{(+⌿ω)÷≢ω}
It is unnamed: the enclosing braces mark it as a function definition. It can be assigned a name for use later, or used anonymously in a more complex expression.
The ω refers to the argument of the function, a list (or 1-dimensional array) of numbers. The ≢ denotes the tally function, which returns here the length of (number of elements in) the argument ω. The divide symbol ÷ has its usual meaning.
The parenthesised +⌿ω denotes the sum of all the elements of ω. The ⌿ operator combines with the + function: the ⌿ fixes the + function between each element of ω, so that
+⌿ 1 2 3 4 5 6 21
is the same as
1+2+3+4+5+6 21
Operators
Operators like ⌿ can be used to derive new functions not only from primitive functions like +, but also from defined functions. For example
{α,', ',ω}⌿
will transform a list of strings representing words into a comma-separated list:
{⍺,', ',⍵}⌿'cow' 'sheep' 'cat' 'dog'
┌────────────────────┐
│cow, sheep, cat, dog│
└────────────────────┘
So back to our mean example. (+⌿ω) gives the sum of the list, which is then divided by ≢ω, the number elements in it.
{(+⌿)÷≢ω} 3 4.5 7 21
8.875
Tacit programming
- Main article: Tacit
In APL’s tacit definition, no braces are needed to mark the definition of a function: primitive functions just combine in a way that enables us to omit any reference to the function arguments — hence tacit. Here is the same calculation written tacitly:
(+⌿÷≢) 3 4.5 7 21 8.875
The operator ⌿ can also be used to modify the (+⌿÷≢) function to produce a moving average.
2 (+⌿÷≢)/ 3 4.5 7 21 3.75 5.75 14
or, more verbosely
ave ← +⌿÷≢
ave 3 4.5 7 21
8.875
mave ← ave⌿
2 mave 3 4.5 7 21
3.75 5.75 14
Text processing
APL represents text as character lists (vectors), making many text operations trivial.
Split text by delimiter
≠ gives 1 for true and 0 for false. It pairs up a single element argument with all the elements of the other arguments:
','≠'comma,delimited,text' 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1
⊢ returns its right argument:
','⊢'comma,delimited,text' comma,delimited,text
⊆ returns a list of runs as indicated by runs of 1s, leaving out elements indicated by 0s:
1 1 0 1 1 1⊆'Hello!' ┌──┬───┐ │He│lo!│ └──┴───┘
We use the comparison vector to partition the right argument:
','(≠⊆⊢)'comma,delimited,text' ┌─────┬─────────┬────┐ │comma│delimited│text│ └─────┴─────────┴────┘
Notice of you can read the tacit function ≠⊆⊢ like an English sentence: The inequality partitions the right argument.
Indices of multiple elements
∊ gives us a mask for elements (characters) in the left argument that are members of the right argument:
'mississippi'∊'sp' 0 0 1 1 0 1 1 0 1 1 0
⍸ gives us the indices where true (1):
⍸'mississippi'∊'sp' 3 4 6 7 9 10
We can combine this into an anonymous infix (dyadic) function:
'mississippi' (⍸∊) 'sp' 3 4 6 7 9 10
Parenthesis nesting level
First we compare all characters to the opening and closing characters;
'()'∘.='plus(square(a),plus(square(b),times(2,plus(a,b)))' 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1
An opening increases the current level, while a closing decreases, so we convert this to changes (or deltas) by subtracting the bottom row from the top row:
-⌿'()'∘.='plus(square(a),plus(square(b),times(2,plus(a,b)))' 0 0 0 0 1 0 0 0 0 0 0 1 0 ¯1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 ¯1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 ¯1 ¯1 ¯1
The running sum is what we're looking for:
+\-⌿'()'∘.='plus(square(a),plus(square(b),times(2,plus(a,b)))' 0 0 0 0 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 2 2 2 2 2 2 2 3 3 2 2 2 2 2 2 2 3 3 3 3 3 3 3 4 4 4 4 3 2 1
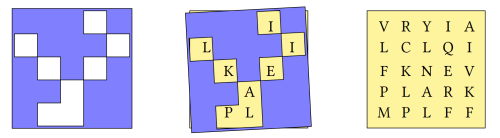
Grille cypher
A grille is a 500 year old method for encrypting messages.
Represent both the grid of letters and the grille as character matrices.
⎕←(grid grille)←5 5∘⍴¨'VRYIALCLQIFKNEVPLARKMPLFF' '⌺⌺⌺ ⌺ ⌺⌺⌺ ⌺ ⌺ ⌺⌺⌺ ⌺⌺⌺ ⌺⌺' ┌─────┬─────┐ │VRYIA│⌺⌺⌺ ⌺│ │LCLQI│ ⌺⌺⌺ │ │FKNEV│⌺ ⌺ ⌺│ │PLARK│⌺⌺ ⌺⌺│ │MPLFF│⌺ ⌺⌺│ └─────┴─────┘
Retrieve elements of the grid where there are spaces in the grille.
grid[⍸grille=' '] ILIKEAPL
An alternative method using ravel.
(' '=,grille)/,grid
ILIKEAPL
| APL development [edit] | |
|---|---|
| Interface | Session ∙ Typing glyphs (on Linux) ∙ Fonts ∙ Text editors |
| Publications | Introductions ∙ Learning resources ∙ Simple examples ∙ Advanced examples ∙ Mnemonics ∙ ISO 8485:1989 ∙ ISO/IEC 13751:2001 ∙ A Dictionary of APL ∙ Case studies ∙ Documentation suites ∙ Books ∙ Papers ∙ Videos ∙ APL Quote Quad ∙ Vector journal ∙ Terminology (Chinese, German) ∙ Neural networks ∙ Error trapping with Dyalog APL (in forms) |
| Sharing code | Backwards compatibility ∙ APLcart ∙ APLTree ∙ APL-Cation ∙ Dfns workspace ∙ Tatin ∙ Cider |
| Implementation | Resources ∙ Open-source ∙ Magic function ∙ Performance ∙ APL hardware |
| Developers | Timeline of corporations ∙ APL2000 ∙ Dyalog ∙ IBM ∙ IPSA ∙ STSC |