Function composition: Difference between revisions
(add comb log eqv.) |
|||
| (15 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
'''Function composition''' refers to the "gluing" together of two [[function]]s using a [[dyadic operator]] such that the functions are applied to the [[argument]](s) as normal, but in a particular pattern | '''Function composition''' refers to the "gluing" together of two or more [[function]]s using a [[dyadic operator]] or a [[train]] such that the functions are applied to the [[argument]](s) as normal, but in a particular pattern. The term [[wikipedia:function composition|function composition]] comes from [[traditional mathematics]] where it is used for a function <math>h(x)=f(g(x))</math> when written as <math> h(x) = (f \circ g)(x)</math>. APL generalises this idea to [[dyadic function]]s, allowing various patterns of application in addition to the simple application of one [[monadic function]] to the result of another monadic function. | ||
== Common compositions == | |||
[[Reverse Compose]] and [[Beside]] treat their arguments in an asymmetric way. They can be seen as using a [[monadic function]] to pre-process the left or right argument, respectively, before proceeding to apply a main function. Their patterns can be visualised as follows: | |||
:[[File: | {| class=wikitable | ||
! Reverse Compose !! Beside | |||
|- | |||
|[[File:F⍛g.png|frameless|200px]]||[[File:F∘g.png|frameless|200px]] | |||
|} | |||
[[Atop (operator)|Atop]] and [[Over]] treat their arguments in a symmetric way. They can be seen as using a monadic function to post-process the result or pre-process the argument(s) of a main function. Their patterns can be visualised as follows: | |||
{| class=wikitable | |||
! Atop !! Over | |||
|- | |||
|[[File:F⍤g.png|frameless|200px]]||[[File:F⍥g.png|frameless|200px]] | |||
|} | |||
[[Tacit_programming#trains|Trains]] provide a way to apply a function to the result(s) of one (for 2-trains) or two (for 3-trains) other functions. These patterns are also called Atop and Fork, and can be visualised as follows: | |||
{| class=wikitable | |||
! 2-train !! 3-train | |||
|- | |||
|[[File:Fg.png|frameless|200px]]||[[File:Fgh.png|frameless|200px]] | |||
|} | |||
The operator represented by [[Jot]] (<syntaxhighlight lang=apl inline>∘</syntaxhighlight>, in this context called [[Bind]]) and the 3-train can also be used with constant arrays, then treating the arrays (<syntaxhighlight lang=apl inline>A</syntaxhighlight>) as constant functions, much as if they were used as operands to the [[Constant]] operator (<syntaxhighlight lang=apl inline>A⍨</syntaxhighlight>): | |||
{| class=wikitable | |||
! Bind !! 3-train | |||
|- | |||
|[[File:A∘g;g∘A.png|frameless|200px]]||[[File:Agh.png|frameless|200px]] | |||
|} | |||
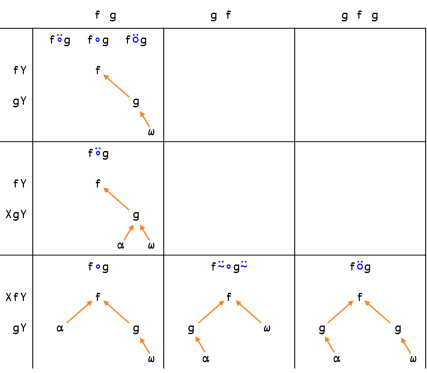
=== Summary of rules === | |||
The above compositions can be summarised as follows, including their [[wikipedia:combinatory logic|combinatory logic]] equivalents: | |||
{| class=wikitable | |||
! Tacit form !! Explicit form !! Function Abstraction !! Symbol !! Bird Name | |||
|- | |||
| <syntaxhighlight lang=apl inline> (f⍛g ) ⍵</syntaxhighlight> || <syntaxhighlight lang=apl inline>( f ⍵) g ⍵ </syntaxhighlight> || λabc.a(bc)c || style="text-align:center" | Σ || Violet Starling | |||
|- | |||
| <syntaxhighlight lang=apl inline>⍺ (f⍛g ) ⍵</syntaxhighlight> || <syntaxhighlight lang=apl inline>( f ⍺) g ⍵ </syntaxhighlight> || λabcd.a(bc)d || style="text-align:center" | Δ || Zebra Dove | |||
|- | |||
| <syntaxhighlight lang=apl inline> ( g∘h) ⍵</syntaxhighlight> || <syntaxhighlight lang=apl inline> g ( h ⍵)</syntaxhighlight> || λabc.a(bc) || style="text-align:center" | B || Bluebird | |||
|- | |||
| <syntaxhighlight lang=apl inline>⍺ ( g∘h) ⍵</syntaxhighlight> || <syntaxhighlight lang=apl inline> ⍺ g ( h ⍵)</syntaxhighlight> || λabcd.ab(cd) || style="text-align:center" | D ||| Dove | |||
|- | |||
| | |||
|- | |||
| <syntaxhighlight lang=apl inline> ( g⍤h) ⍵</syntaxhighlight> || <syntaxhighlight lang=apl inline> g ( h ⍵)</syntaxhighlight> || λabc.a(bc) || style="text-align:center" | B || Bluebird | |||
|- | |||
| <syntaxhighlight lang=apl inline>⍺ ( g⍤h) ⍵</syntaxhighlight> || <syntaxhighlight lang=apl inline> g (⍺ h ⍵)</syntaxhighlight> || λabcd.a(bcd) || style="text-align:center" | B<sub>1</sub> || Blackbird | |||
|- | |||
| <syntaxhighlight lang=apl inline> ( g⍥h) ⍵</syntaxhighlight> || <syntaxhighlight lang=apl inline> g ( h ⍵)</syntaxhighlight> || λabc.a(bc) || style="text-align:center" | B || Bluebird | |||
|- | |||
| <syntaxhighlight lang=apl inline>⍺ ( g⍥h) ⍵</syntaxhighlight> || <syntaxhighlight lang=apl inline>( h ⍺) g ( h ⍵)</syntaxhighlight> || λabcd.a(bc)(bd) || style="text-align:center" | Ψ || | |||
|- | |||
| | |||
|- | |||
| <syntaxhighlight lang=apl inline> ( g h) ⍵</syntaxhighlight> || <syntaxhighlight lang=apl inline> g ( h ⍵)</syntaxhighlight> || λabc.a(bc) || style="text-align:center" | B || Bluebird | |||
|- | |||
| <syntaxhighlight lang=apl inline>⍺ ( g h) ⍵</syntaxhighlight> || <syntaxhighlight lang=apl inline> g (⍺ h ⍵)</syntaxhighlight> || λabcd.a(bcd) || style="text-align:center" | B<sub>1</sub> || Blackbird | |||
|- | |||
| <syntaxhighlight lang=apl inline> (f g h) ⍵</syntaxhighlight> || <syntaxhighlight lang=apl inline>( f ⍵) g ( h ⍵)</syntaxhighlight> || λabcd.a(bd)(cd) || style="text-align:center" | Φ || Phoenix | |||
|- | |||
| <syntaxhighlight lang=apl inline>⍺ (f g h) ⍵</syntaxhighlight> || <syntaxhighlight lang=apl inline>(⍺ f ⍵) g (⍺ h ⍵)</syntaxhighlight> || λabcde.a(bde)(cde) || style="text-align:center" | Φ<sub>1</sub> || Pheasant | |||
|- | |||
| | |||
|- | |||
| <syntaxhighlight lang=apl inline> (A∘g ) ⍵</syntaxhighlight> || <syntaxhighlight lang=apl inline> A g ⍵ </syntaxhighlight> || || || | |||
|- | |||
| <syntaxhighlight lang=apl inline> ( g∘A) ⍵</syntaxhighlight> || <syntaxhighlight lang=apl inline> ⍵ g A </syntaxhighlight> || || || | |||
|- | |||
| <syntaxhighlight lang=apl inline> (A g h) ⍵</syntaxhighlight> || <syntaxhighlight lang=apl inline> A g ( h ⍵)</syntaxhighlight> || || || | |||
|- | |||
| <syntaxhighlight lang=apl inline>⍺ (A g h) ⍵</syntaxhighlight> || <syntaxhighlight lang=apl inline> A g (⍺ h ⍵)</syntaxhighlight> || || || | |||
|} | |||
== Additional compositions == | == Additional compositions == | ||
Additional compositions are possible, even without using an argument more than once or applying a function to its own result. However, most of these are rather trivial shuffled-around versions of the above three. For example, one could define an operator identical to Atop, only that it applies the right operand to the result of the left operand, that is < | Additional compositions are possible, even without using an argument more than once or applying a function to its own result. However, most of these are rather trivial shuffled-around versions of the above three. For example, one could define an operator identical to Atop, only that it applies the right operand to the result of the left operand, that is <syntaxhighlight lang=apl inline>{⍵⍵ ⍺ ⍺⍺ ⍵}</syntaxhighlight>. | ||
When Dyalog added Atop and Over, it was with the reasoning that these were the only compositions where the leftmost function acted as the "root" function in the evaluation tree, while the arguments were used each on their respective sides of the constituent functions: | |||
[[File:AllCompositions.png|427px]] | |||
Of note is [[Reverse-compose]] < | Of note here is <syntaxhighlight lang=apl inline>f⍨∘g⍨</syntaxhighlight> which is equivalent to — although with swapped operands — [[Reverse-compose]] <syntaxhighlight lang=apl inline>⍛</syntaxhighlight> (also called ''Before''), and the mirrored version of Beside <syntaxhighlight lang=apl inline>∘</syntaxhighlight> (also known as ''Compose'' and ''After''), because it is the only such variation that has been implemented, namely in [[dzaima/APL]] and [[Extended Dyalog APL]]. | ||
A compositional operator that isn't just a shuffled around version of the basic three, is one that applies one operand between the other operand's dyadic result and the result of that other operand's result when [[swap]]ped: < | A compositional operator that isn't just a shuffled around version of the basic three, is one that applies one operand between the other operand's dyadic result and the result of that other operand's result when [[swap]]ped: <syntaxhighlight lang=apl inline>{(⍵ ⍵⍵ ⍺) ⍺⍺ (⍺ ⍵⍵ ⍵)}</syntaxhighlight>. This operator can for example be used to implement [[wikipedia:three-way comparison|three-way comparison]]: | ||
[https://tio.run/##SyzI0U2pTMzJT///P1jhUdsEhWqNR71bFYAYQu3SBBFApKABIuDiWzVruZJzC8BadIMfdS7hetQ3FcQxUjBWMFEASRn//w8A Try it online!]< | [https://tio.run/##SyzI0U2pTMzJT///P1jhUdsEhWqNR71bFYAYQu3SBBFApKABIuDiWzVruZJzC8BadIMfdS7hetQ3FcQxUjBWMFEASRn//w8A Try it online!]<syntaxhighlight lang=apl> | ||
S ← {(⍵ ⍵⍵ ⍺) ⍺⍺ (⍺ ⍵⍵ ⍵)} | S ← {(⍵ ⍵⍵ ⍺) ⍺⍺ (⍺ ⍵⍵ ⍵)} | ||
cmp ← -S≤ | cmp ← -S≤ | ||
| Line 20: | Line 95: | ||
4 cmp 3 | 4 cmp 3 | ||
1 | 1 | ||
</ | </syntaxhighlight>{{Works in|[[Dyalog APL]], [[NARS2000]], [[ngn/apl]]}} | ||
== External links == | == External links == | ||
* [[Dyalog '19]]: [https://dyalog.tv/Dyalog19/?v=czWC4tjwzOQ Tacit Techniques with Dyalog version 18.0 Operators] | * [[Dyalog '19]]: [https://dyalog.tv/Dyalog19/?v=czWC4tjwzOQ Tacit Techniques with Dyalog version 18.0 Operators] | ||
* [[Dyalog webinar]]: [https://dyalog.tv/Webinar/?v=Hln3zryunsw Language Features of Dyalog version 18.0 in Depth] | * [[Dyalog webinar]]: [https://dyalog.tv/Webinar/?v=Hln3zryunsw Language Features of Dyalog version 18.0 in Depth] | ||
{{APL | * Conor Hoekstra: [https://raw.githubusercontent.com/codereport/Content/main/Publications/Combinatory_Logic_and_Combinators_in_Array_Languages.pdf Combinatory Logic and Combinators in Array Languages] | ||
{{APL features}}[[Category:Composition operators]][[Category:Tacit programming]] | |||
Latest revision as of 17:07, 29 May 2024
Function composition refers to the "gluing" together of two or more functions using a dyadic operator or a train such that the functions are applied to the argument(s) as normal, but in a particular pattern. The term function composition comes from traditional mathematics where it is used for a function when written as . APL generalises this idea to dyadic functions, allowing various patterns of application in addition to the simple application of one monadic function to the result of another monadic function.
Common compositions
Reverse Compose and Beside treat their arguments in an asymmetric way. They can be seen as using a monadic function to pre-process the left or right argument, respectively, before proceeding to apply a main function. Their patterns can be visualised as follows:
| Reverse Compose | Beside |
|---|---|
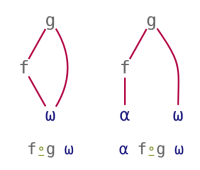 |
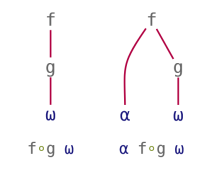
|
Atop and Over treat their arguments in a symmetric way. They can be seen as using a monadic function to post-process the result or pre-process the argument(s) of a main function. Their patterns can be visualised as follows:
| Atop | Over |
|---|---|
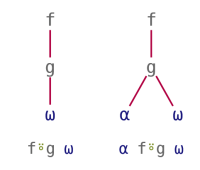 |
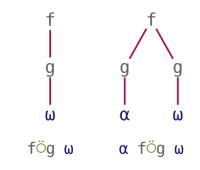
|
Trains provide a way to apply a function to the result(s) of one (for 2-trains) or two (for 3-trains) other functions. These patterns are also called Atop and Fork, and can be visualised as follows:
| 2-train | 3-train |
|---|---|
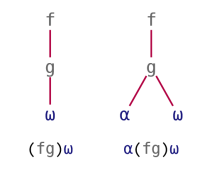 |
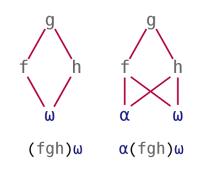
|
The operator represented by Jot (∘, in this context called Bind) and the 3-train can also be used with constant arrays, then treating the arrays (A) as constant functions, much as if they were used as operands to the Constant operator (A⍨):
| Bind | 3-train |
|---|---|
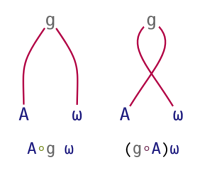 |
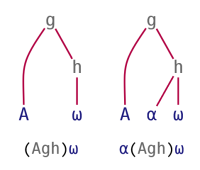
|
Summary of rules
The above compositions can be summarised as follows, including their combinatory logic equivalents:
| Tacit form | Explicit form | Function Abstraction | Symbol | Bird Name |
|---|---|---|---|---|
(f⍛g ) ⍵ |
( f ⍵) g ⍵ |
λabc.a(bc)c | Σ | Violet Starling |
⍺ (f⍛g ) ⍵ |
( f ⍺) g ⍵ |
λabcd.a(bc)d | Δ | Zebra Dove |
( g∘h) ⍵ |
g ( h ⍵) |
λabc.a(bc) | B | Bluebird |
⍺ ( g∘h) ⍵ |
⍺ g ( h ⍵) |
λabcd.ab(cd) | D | Dove |
( g⍤h) ⍵ |
g ( h ⍵) |
λabc.a(bc) | B | Bluebird |
⍺ ( g⍤h) ⍵ |
g (⍺ h ⍵) |
λabcd.a(bcd) | B1 | Blackbird |
( g⍥h) ⍵ |
g ( h ⍵) |
λabc.a(bc) | B | Bluebird |
⍺ ( g⍥h) ⍵ |
( h ⍺) g ( h ⍵) |
λabcd.a(bc)(bd) | Ψ | |
( g h) ⍵ |
g ( h ⍵) |
λabc.a(bc) | B | Bluebird |
⍺ ( g h) ⍵ |
g (⍺ h ⍵) |
λabcd.a(bcd) | B1 | Blackbird |
(f g h) ⍵ |
( f ⍵) g ( h ⍵) |
λabcd.a(bd)(cd) | Φ | Phoenix |
⍺ (f g h) ⍵ |
(⍺ f ⍵) g (⍺ h ⍵) |
λabcde.a(bde)(cde) | Φ1 | Pheasant |
(A∘g ) ⍵ |
A g ⍵ |
|||
( g∘A) ⍵ |
⍵ g A |
|||
(A g h) ⍵ |
A g ( h ⍵) |
|||
⍺ (A g h) ⍵ |
A g (⍺ h ⍵) |
Additional compositions
Additional compositions are possible, even without using an argument more than once or applying a function to its own result. However, most of these are rather trivial shuffled-around versions of the above three. For example, one could define an operator identical to Atop, only that it applies the right operand to the result of the left operand, that is {⍵⍵ ⍺ ⍺⍺ ⍵}.
When Dyalog added Atop and Over, it was with the reasoning that these were the only compositions where the leftmost function acted as the "root" function in the evaluation tree, while the arguments were used each on their respective sides of the constituent functions:
Of note here is f⍨∘g⍨ which is equivalent to — although with swapped operands — Reverse-compose ⍛ (also called Before), and the mirrored version of Beside ∘ (also known as Compose and After), because it is the only such variation that has been implemented, namely in dzaima/APL and Extended Dyalog APL.
A compositional operator that isn't just a shuffled around version of the basic three, is one that applies one operand between the other operand's dyadic result and the result of that other operand's result when swapped: {(⍵ ⍵⍵ ⍺) ⍺⍺ (⍺ ⍵⍵ ⍵)}. This operator can for example be used to implement three-way comparison:
S ← {(⍵ ⍵⍵ ⍺) ⍺⍺ (⍺ ⍵⍵ ⍵)}
cmp ← -S≤
2 cmp 3
¯1
3 cmp 3
0
4 cmp 3
1
External links
- Dyalog '19: Tacit Techniques with Dyalog version 18.0 Operators
- Dyalog webinar: Language Features of Dyalog version 18.0 in Depth
- Conor Hoekstra: Combinatory Logic and Combinators in Array Languages
| APL features [edit] | |
|---|---|
| Built-ins | Primitives (functions, operators) ∙ Quad name |
| Array model | Shape ∙ Rank ∙ Depth ∙ Bound ∙ Index (Indexing) ∙ Axis ∙ Ravel ∙ Ravel order ∙ Element ∙ Scalar ∙ Vector ∙ Matrix ∙ Simple scalar ∙ Simple array ∙ Nested array ∙ Cell ∙ Major cell ∙ Subarray ∙ Empty array ∙ Prototype |
| Data types | Number (Boolean, Complex number) ∙ Character (String) ∙ Box ∙ Namespace ∙ Function array |
| Concepts and paradigms | Conformability (Scalar extension, Leading axis agreement) ∙ Scalar function (Pervasion) ∙ Identity element ∙ Complex floor ∙ Array ordering (Total) ∙ Tacit programming (Function composition, Close composition) ∙ Glyph ∙ Leading axis theory ∙ Major cell search ∙ First-class function |
| Errors | LIMIT ERROR ∙ RANK ERROR ∙ SYNTAX ERROR ∙ DOMAIN ERROR ∙ LENGTH ERROR ∙ INDEX ERROR ∙ VALUE ERROR ∙ EVOLUTION ERROR |