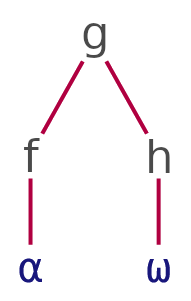
Split composition
f⍛g∘h
|
Split composition is a tacit pattern, used to pre-process argument(s) with the outer-most operands before applying the middle operand between the result. Given functions f, g, and h, a split composition on arguments x and y is defined as (f x) g (h y).
This construct was introduced by the I language as "split-compose", where it is represented with O which also represents the Over operator - as it too is a split composition with identical outer operands.
This doesn't appear as a primitive in any APL, nor can it, because it composes three functions, while a compositional operator can take no more than two operands. This situation is identical to that of the fork. Both split compositions and forks can be constructed using companion operators, tying together the three involved functions.
In Extended Dyalog APL and dzaima/APL, a split composition can be formed using Reverse Compose (⍛) and Compose (∘). In this example, we multiply the interval (integers up until) of the left argument, with the Magnitude of the right:
5 ⍳⍛×∘| 5 ¯8 ¯2 ¯5 3 5 16 6 20 15
This is evaluated as (⍳5) × (|5 ¯8 ¯2 ¯5 3). A further example concatenates the reciprocal of the left argument with the negation of the right:
2 ÷⍛,- 4 0.5 ¯4
This is evaluated as (÷2) × (-4).
Alternatives
In dialects that lack Reverse Compose (and even Compose), split compositions can be denoted either by defining the missing operator(s), or as a single derived function or fork, if this is supported. For example, in Dyalog APL the pattern can be formed with Compose and Commute (⍨) as g⍨∘f⍨∘h:
5 ×⍨∘⍳⍨∘| 5 ¯8 ¯2 ¯5 3
5 16 6 20 15
2(,⍨∘÷⍨∘-)4
0.5 ¯4
Note that g∘h⍨∘f⍨ applies f before h which can matter for functions with side effects. For example, consider the following where 'x' f⍛g∘h 'y' would print hfg:
f←{⍞←⊃⎕SI}
g←{⍞←⊃⎕SI}
h←{⍞←⊃⎕SI}
'x' g⍨∘f⍨∘h 'y'
hfg
'x' g∘h⍨∘f⍨ 'y'
fhg
The equivalent fork is f⍤⊣ g h⍤⊢, for example:
5 (⍳⍤⊣×|⍤⊢) 5 ¯8 ¯2 ¯5 3
5 16 6 20 15
2(÷⍤⊣,-⍤⊢)4
0.5 ¯4