Array notation

Array notation is a way to write most arrays literally, with no or minimal use of primitive functions, possibly over multiple code lines. While APL has had at least simple numeric strand notation since APL\360, no major APL has implemented native support for an extended notation as of 2020.

Railroad diagram for the array notation syntax.

Medium-sized array constants are often needed in code. Due to the lack of a native multi-line notation, programmers have resorted to various ad-hoc methods of approximating such, usually at the cost of reduced readability. A very common technique is repeated concatenation:

poss←1 2⍴'fns'  ((0 1)(0.7 0)(0.7 0)×size)
poss⍪←   'fnd'  ((0 1)(0   0)(0   0)×size)
poss⍪←   'lines'((0 0)(0.7 0)(0.7 0)×size)
poss⍪←   'lnd'  ((0 0)(0   0)(0   0)×size)

Using the array notation described in this article, the array could for example be written as:

poss←['fns'  ((0 1)(0.7 0)(0.7 0)×size)
      'fnd'  ((0 1)(0   0)(0   0)×size)
      'lines'((0 0)(0.7 0)(0.7 0)×size)
      'lnd'  ((0 0)(0   0)(0   0)×size)]

The array notation can also be used to express the inner vectors of vectors:

poss←['fns'  ((0 1 ⋄ 0.7 0 ⋄ 0.7 0)×size)
      'fnd'  ((0 1 ⋄ 0   0 ⋄ 0   0)×size)
      'lines'((0 0 ⋄ 0.7 0 ⋄ 0.7 0)×size)
      'lnd'  ((0 0 ⋄ 0   0 ⋄ 0   0)×size)]

Description

The notation is added to the language by giving meaning to previously invalid statements. The added syntax consists of three constructs that are currently SYNTAX ERRORs:

• broken round parentheses
• broken square brackets
• empty round parentheses: ()

where broken means interrupted by one or more diamonds (⋄) or line breaks (outside of dfns).

• A broken round parenthesis creates a vector, where every diamond/line break-separated statement forms an element in the resulting vector.
• A broken square bracket creates a an array, where every diamond/line break-separated statement forms a major cell in the resulting array.
• () is equivalent to (⎕NS 0⍴⊂'')

Formal syntax

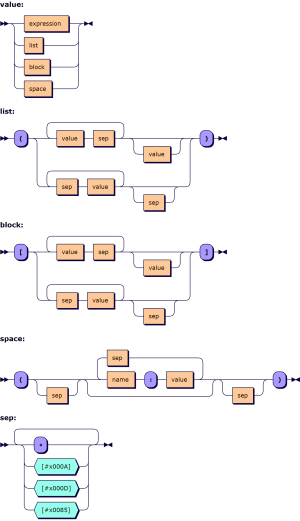
The array notation can be described using Extended Backus–Naur form, where an expression is any traditional APL expression:

value    ::= expression | list | block | space
list     ::= '(' ( ( value sep )+ value? | ( sep value )+ sep? ) ')'
block    ::= '[' ( ( value sep )+ value? | ( sep value )+ sep? ) ']'
space    ::= '(' sep? ( name ':' value ( sep name ':' value )* )? sep? ')'
sep      ::= [⋄#x000A#x000D#x0085]+

History

Array notation in NARS.

1981

When NARS introduced nested array theory, the need for a way to represent complex structures was already recognised. Though a formal notation was never adopted, much less implemented, the NARS reference manual included round parentheses to delimit nested arrays.

2014

At Dyalog '14, Morten Kromberg said:

The emphasis on using scripts to store source code means that it's probably time for us to come up with a notation for constants in the language so that in your script you can declare matrices and so on in a nice readable fashion.

Although no concrete proposal was made at the time, he set the expectation of this being the subject of a presentation the following year.

2015

At Dyalog '15, Phil Last explained that he considered the lack of such a notation a big hole in APL notation and gave a suggestions for such a notation. He presented a model using square brackets to indicate collections of major cells of rank 1 or higher, delimited by line breaks and/or diamonds, for example [1 2 3 ⋄ 4 5 6] would be equivalent to 2 3⍴1 2 3 4 5 6. He also proposed that if the delimited expressions were assignments, then the notation would instead declare members of an anonymous namespace, for example for example [a←3 ⋄ b←6]. He pointed out that this overloading of the symbols meant that the array notation could only represent constants, as allowing general expressions would lead to ambiguity. He also mentioned that doubled symbols or Unicode brackets could be used instead.

After the presentation, Phil Last had a conversation with Adám Brudzewsky who had recently joined Dyalog Ltd., the language developer of Dyalog APL, and who was inspired to begin an internal Dyalog research project on the matter. Meanwhile, Acre Desktop, a project manager that Last co-develops, moved from storing APL items in component files to storing them in text files, necessitating a literal notation for arrays, and his notation for arrays was adopted. Acre stores unscripted namespaces as directories, so the need for a literal namespace notation only arises when a namespace is an element in a larger array, something that is quite unlikely for application constants.

2016

Phil Last published a more formal proposal in the Vector Journal. Again, the notation was only described as a serialisation format; not as an integral part of the language. He added escape sequences to strings, further distancing the notation from compatibility with existing APL code.

Array notation at Dyalog '17.

2017

At Dyalog '17, Adám Brudzewsky proposed an alternative notation using round parentheses to indicate collections of major cells of any rank, thus allowing the notation to express nested vectors though scalar major cells, for example (⊂1 2 3 ⋄ ⊂4 5 6) would be equivalent to (1 2 3)(4 5 6). This notation had a striking similarity to the informal notation used in the NARS reference manual over 35 years prior. For namespace, he proposed using colon (:) to delimit name-value pairs, inspired by JSON in which colon is used in the same manner, despite assignment being denoted by = in JavaScript, from which JSON was derived. This distinction allowed arbitrary expressions in arrays, opening the possibility of full integration into the language, while also allowing a namespace with no members to be denoted (). Last's proposal required [:] to distinguish it from bracket indexing into a vector while eliding the indices, a technique used to address all elements.

In addition to the main array notation, Brudzewsky also proposed allowing line breaks between quotes in strings to represent a vector of character vectors (with leading and trailing spaces trimmed). While not included in the live presentation, Brudzewsky's slide deck included a discussion of whether expressions resulting in a scalar should be treated as singleton vectors or not. It concluded that if they were treated as vectors, then an alternative notation in the form of a line continuation character would be necessary to allow writing large vectors over multiple lines of code.

Array notation at Dyalog '18.

2018

At Dyalog '18, Adám Brudzewsky returned with a solution to the issue on whether scalars should be regarded as 1-element vectors (thus increasing the rank of the containing array) or left as scalars (thus forming a vector). He reintroduced square brackets as collections of major cells of rank 1 or higher, repurposing round parentheses as vectors.

The namespace notation remained as before, using round parentheses so the empty namespace could be written in a consistent manner, but he presented formalised scoping rules for the value expressions, namely that these would run in the surrounding namespace, but within their own scope, so any assignment done during such an expression. For example (a:b,b←1 2) would neither populate the new namespace with a member b, nor create such a variable in the global scope. Acre quickly adopted this notation.

Array notation at Dyalog '20

2020

In the spring of 2020, dzaima/APL adopted the proposed array notation with the exception of forcing the result of statements in square brackets to rank 1 or higher.

At Dyalog '20, Adám Brudzewsky presented the notation as Release Candidate 1 and showed how Dyalog APL 18.0's updated version of Link (a simple interface for using source code in text files, synchronising the file system and the workspace) includes experimental support the array notation, including a facility to use multi-line array notation inside functions. He estimated that Dyalog APL 20.0 will include native interpreter support for the notation in 2022.

Design considerations

In creating the notation's specification, various alternatives were considered. The following requirements were proposed:

1. No new glyphs
2. Reusing existing glyphs for similar purposes
3. Similarity to other languages (K, JSON, CSS)
4. Visual attractiveness
5. Intuitive syntax
6. As little syntactic sugar as possible

Glyphs

The design requirement for no new glyphs was contentious, and both bi-glyph and non-ASCII brackets were considered. Bi-glyphs were rejected out of readability concerns, especially when nested. For example, 1 1 3⍴2 could have been written as [[[[2 2 2]]]]. Non-ASCII brackets were rejected for font and keyboarding reasons, as well as to make it easier for non-APL systems to generate APL data. For example, ⟦…⟧ was proposed to denote a collection of major cells, forming a new array of rank one-higher than the rank of the highest-rank constituent cell. However, few fonts support these glyphs.

The eventual choice was to go with existing symbols, and this had important implications for the specifics of the notation. While ideally, a notation would have been introduced for a collection of major cells, thereby handling both vectors and higher-rank arrays, a problem presents itself with axes of length 1, because both square brackets and round parentheses already have meaning with when surrounding a single statement (namely function axis/bracket indexing and precedence/function trains). Thus, while 2 ⟦3⟧ could have denoted the nested array 2 (1⍴3), this isn't viable with 2 [1⍴3] because this already denotes indexing 2 using the indices 1⍴3. To disambiguate, at least one statement separator or line break must be present in each level of array notation brackets and parentheses.

Minimum rank of major cells

While ⟦⟦3⟧⟧ could denote 1 1⍴3 using non-ASCII glyphs, an equivalent ASCII scheme instead would have required [[3⋄]⋄] where the inner bracket creates a vector, and the outer creates a matrix. Using line breaks instead of diamonds, it was found to be counter-intuitive that

[
 3
 5
  ]

was to denote two-element vector while

[
 3 4
 5 6
    ]

would be a two-row matrix. Therefore, a special rule was added to the effect that in such collections of major cells, every cell would be considered to have a rank of at least 1, even if it was a scalar.

In turn, this choice introduced the need for a separate notation to allow vectors to be written over multiple lines, and therefore the round parentheses was extended from its traditional use in strand notation to also denote a collection of enclosed elements.

Name-value pairs

As a notation for namespaces, several details were debated:

1. Whether to use ⋄ or ; to separate name-value pairs (in addition to line breaks)
2. Which enclosure glyphs to use, (…) or […]
3. Which glyph should separate the name from the value, : or ←
4. In which scope the value expressions should be evaluated

The ⋄ was chosen to separate name-value pairs, as it is generally exchangeable with a line break, while ; though it is used to separate names ― without values ― in headers and in locals lines. Furthermore, it was seen as natural the values would be computed in reading order (left-to-right) just like multiple statements are, and while ⋄ would imply this, ; wouldn't. Indeed, in the statement A[B;C], expression C is evaluated before expression B. It was briefly considered to have values computed from the right, just line stranding is, but this was rejected because replacing the semi-colons with line breaks would then require evaluation beginning with the last line and working upwards!

Round parentheses were chosen because namespaces are seen as (unordered) lists, and so are more similar to vectors than higher-rank arrays. Furthermore, [] already had meaning (indexing all elements of a vector) while () didn't have any existing use, and so could be used to denote a new empty namespace, equivalent to ⎕NS 0⍴⊂''.

While initially, ← was seen as the obvious choice to separate the name and the value, it was soon discovered that a namespace with only one member would be indistinguishable from a parenthesised assignment. Furthermore, it was noted that value expressions could contain intermediary assignments, and that such assignments were of a fundamentally different nature from the name-value declaration. The intermediary assignments would happen in a temporary scope, with any created variables disappearing once the namespace member value was established.

Value expressions could be evaluated in the newly established namespace (similar to expressions in :Namespace scripts), or in the surrounding scope (similar to inline expressions in JavaScript's object notation). It was envisioned that a main usage of the literal notation would be to collect existing values into a namespace, and evaluating inside the new namespace would force the use of ##. to fetch values in the surrounding scope. In a departure from JavaScript, it was found most natural that such intermediate assignments be local to the value expression, similar to assignments in dfns. Global assignment is still available using ⎕THIS.name←value, just as in dfns.