Tacit programming: Difference between revisions
m (Fix code) |
|||
| (12 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
'''Tacit programming''', also called '''[[wikipedia:Tacit_programming|point-free style]]''', refers to usage of tacit [[function]]s that are defined in terms of implicit [[argument]]s. This is in contrast to the explicit use of arguments in [[dfn]]s (< | [[File:Function compositions.png|thumb|right|Diagrams of [[function composition]]s, an important part of tacit programming.]] | ||
'''Tacit programming''', also called '''[[wikipedia:Tacit_programming|point-free style]]''', refers to usage of tacit [[function]]s that are defined in terms of implicit [[argument]]s. This is in contrast to the explicit use of arguments in [[dfn]]s (<syntaxhighlight inline lang=apl>⍺ ⍵</syntaxhighlight>) and [[tradfn]]s (which have named arguments). Some APL dialects allow to combine functions into [[train]]s following a small set of rules. This allows creating complex [[derived function]]s without specifying any arguments explicitly. | |||
Dialects which implement trains include [[Dyalog APL]], [[dzaima/APL]], [[ngn/apl]] and [[NARS2000]]. | Dialects which implement trains include [[Dyalog APL]], [[dzaima/APL]], [[ngn/apl]] and [[NARS2000]]. | ||
| Line 5: | Line 6: | ||
== Primitives == | == Primitives == | ||
All [[primitive functions]] are tacit. Some APLs allow primitive functions to be named. | All [[primitive functions]] are tacit. Some APLs allow primitive functions to be named. | ||
< | <syntaxhighlight lang=apl> | ||
plus ← + | plus ← + | ||
times ← × | times ← × | ||
6 times 3 plus 5 | 6 times 3 plus 5 | ||
48 | 48 | ||
</ | </syntaxhighlight> | ||
== Derived functions == | == Derived functions == | ||
Functions derived from a monadic operator and an operand, or from a dyadic operator and two operands are tacit functions: | Functions derived from a monadic operator and an operand, or from a dyadic operator and two operands are tacit functions: | ||
< | <syntaxhighlight lang=apl> | ||
Sum ← +/ | Sum ← +/ | ||
Sum ⍳10 | Sum ⍳10 | ||
| Line 20: | Line 21: | ||
Dot ← +.× | Dot ← +.× | ||
3 1 4 | 3 1 4 Dot 2 7 1 | ||
17 | 17 | ||
</ | </syntaxhighlight> | ||
== Derived operators == | == Derived operators == | ||
A dyadic operator with its right operand forms a tacit monadic operator: | A dyadic operator with its right operand forms a tacit monadic operator: | ||
< | <syntaxhighlight lang=apl> | ||
1(+⍣2)10 | 1(+⍣2)10 | ||
12 | 12 | ||
| Line 31: | Line 33: | ||
1 +Twice 10 | 1 +Twice 10 | ||
12 | 12 | ||
</ | </syntaxhighlight> | ||
== Trains == | == Trains == | ||
A train is a series of functions in isolation. An isolated function is either surrounded by parentheses or named. | A [[train]] is a series of functions in isolation. An isolated function is either surrounded by parentheses or named. | ||
These rules are used for 3-trains, called [[fork]]s: | |||
{| | {| | ||
|< | |<syntaxhighlight lang=apl> (f g h) ⍵</syntaxhighlight>|| {{←→}} ||<syntaxhighlight lang=apl>( f ⍵) g ( h ⍵)</syntaxhighlight> | ||
|- | |- | ||
|< | |<syntaxhighlight lang=apl>⍺ (f g h) ⍵</syntaxhighlight>|| {{←→}} ||<syntaxhighlight lang=apl>(⍺ f ⍵) g (⍺ h ⍵)</syntaxhighlight> | ||
|} | |} | ||
The ''left tine'' of a fork can be an array: | The ''left tine'' of a fork can be an array: | ||
{| | {| | ||
|< | |<syntaxhighlight lang=apl> (A g h) ⍵</syntaxhighlight>|| {{←→}} ||<syntaxhighlight lang=apl>A g ( h ⍵)</syntaxhighlight> | ||
|- | |- | ||
|< | |<syntaxhighlight lang=apl>⍺ (A g h) ⍵</syntaxhighlight>|| {{←→}} ||<syntaxhighlight lang=apl>A g (⍺ h ⍵)</syntaxhighlight> | ||
|} | |} | ||
In APL (but not [[J]]), these rules are used for 2-trains, called [[atop]]s: | |||
{| | {| | ||
|< | |<syntaxhighlight lang=apl> (g h) ⍵</syntaxhighlight>|| {{←→}} ||<syntaxhighlight lang=apl>g ( h ⍵)</syntaxhighlight> | ||
|- | |- | ||
|< | |<syntaxhighlight lang=apl>⍺ (g h) ⍵</syntaxhighlight>|| {{←→}} ||<syntaxhighlight lang=apl>g (⍺ h ⍵)</syntaxhighlight> | ||
|} | |} | ||
Any train can be expressed in terms of [[function composition]] — except dyadic forks. Some common patterns are: | |||
{| | {| | ||
|< | |<syntaxhighlight lang=apl>(f g h) ⍵</syntaxhighlight>|| {{←→}} ||<syntaxhighlight lang=apl>g⍨∘f⍨∘h⍨ ⍵</syntaxhighlight> | ||
|- | |||
|<syntaxhighlight lang=apl>(f g f) ⍵</syntaxhighlight>|| {{←→}} ||<syntaxhighlight lang=apl>g⍥f⍨ ⍵</syntaxhighlight> | |||
|- | |- | ||
|< | |<syntaxhighlight lang=apl>(⊢ g f) ⍵</syntaxhighlight>|| {{←→}} ||<syntaxhighlight lang=apl>g∘f⍨ ⍵</syntaxhighlight> | ||
|} | |} | ||
== Debugging == | == Debugging == | ||
In [[Dyalog APL]], analysis of trains is assisted by a [[user command]] < | In [[Dyalog APL]], analysis of trains is assisted by a [[user command]] <syntaxhighlight lang=apl inline>]Boxing on</syntaxhighlight>. This is achieved by executing the command <syntaxhighlight lang=apl inline>]Boxing on</syntaxhighlight> and then entering a train without any parameters. A structure of the train will be displayed. | ||
For example, the "accursed train" from the section below can be analysed like this: | For example, the "accursed train" from the section below can be analysed like this: | ||
< | <syntaxhighlight lang=apl> | ||
]Boxing on | ]Boxing on | ||
Was OFF | Was OFF | ||
| Line 93: | Line 87: | ||
│└───────────┴─────────────────┘│ │ | │└───────────┴─────────────────┘│ │ | ||
└───────────────────────────────┴───────┘ | └───────────────────────────────┴───────┘ | ||
</ | </syntaxhighlight> | ||
Alternatively, a train can be represented in form of a tree: | Alternatively, a train can be represented in form of a tree: | ||
< | <syntaxhighlight lang=apl> | ||
]Boxing on -trains=tree | ]Boxing on -trains=tree | ||
Was ON -trains=box | Was ON -trains=box | ||
| Line 108: | Line 102: | ||
+ × ┌┴┐ | + × ┌┴┐ | ||
∘ × | ∘ × | ||
</ | </syntaxhighlight> | ||
Or fully parenthesised: | Or fully parenthesised: | ||
< | <syntaxhighlight lang=apl> | ||
]Boxing on -trains=parens | ]Boxing on -trains=parens | ||
Was OFF -trains=box | Was OFF -trains=box | ||
((+.×⍨⊢~∘.×⍨)1↓⍳) ⍝ the train to be analysed | ((+.×⍨⊢~∘.×⍨)1↓⍳) ⍝ the train to be analysed | ||
(((+.×)⍨)(⊢~((∘.×)⍨)))(1↓⍳) | (((+.×)⍨)(⊢~((∘.×)⍨)))(1↓⍳) | ||
</ | </syntaxhighlight> | ||
=== Conversion to dfns === | === Conversion to dfns === | ||
It can help understanding to convert a tacit function to a dfn. For many tacit functions, it is not immediately clear if the intention of the function is to be used monadically or dyadically, or even both. Such knowledge can be conveyed by comments, but sometimes it is possible to spot patterns that are exclusively monadic or dyadic: A function with a bound argument (for example < | It can help understanding to convert a tacit function to a dfn. For many tacit functions, it is not immediately clear if the intention of the function is to be used monadically or dyadically, or even both. Such knowledge can be conveyed by comments, but sometimes it is possible to spot patterns that are exclusively monadic or dyadic: A function with a bound argument (for example <syntaxhighlight lang=apl inline>+∘1</syntaxhighlight>) can indicate a monadic function, and in some contexts, <syntaxhighlight lang=apl inline>=</syntaxhighlight>, which can only be used dyadically, would indicate a dyadic function. The website [https://tacit.help tacit.help] provides automated translation of most tacit functions, into both monadic and dyadic, fully parenthesised dfns. | ||
== Examples == | == Examples == | ||
One of the major benefits of tacit programming is the ability to convey a short, well-defined idea as an isolated expression. This aids both human readability ([[semantic density]]) and the computer's ability to interpret code, potentially executing special code for particular [[idiom]]s. | One of the major benefits of tacit programming is the ability to convey a short, well-defined idea as an isolated expression. This aids both human readability ([[semantic density]]) and the computer's ability to interpret code, potentially executing special code for particular [[idiom]]s. | ||
=== Plus and minus === | === Plus and minus === | ||
< | <syntaxhighlight lang=apl> | ||
(+,-) 2 ⍝ ±2 | (+,-) 2 ⍝ ±2 | ||
2 ¯2 | 2 ¯2 | ||
5 (+,-) 2 ⍝ 5±2 | 5 (+,-) 2 ⍝ 5±2 | ||
7 3 | 7 3 | ||
</ | </syntaxhighlight> | ||
=== Arithmetic mean === | === Arithmetic mean === | ||
< | <syntaxhighlight lang=apl> | ||
(+⌿÷≢) ⍳10 ⍝ Mean of the first ten integers | (+⌿÷≢) ⍳10 ⍝ Mean of the first ten integers | ||
5.5 | 5.5 | ||
(+⌿÷≢) 5 4⍴⍳4 ⍝ Mean of columns in a matrix | (+⌿÷≢) 5 4⍴⍳4 ⍝ Mean of columns in a matrix | ||
1 2 3 4 | 1 2 3 4 | ||
</ | </syntaxhighlight> | ||
=== Fractions === | === Fractions === | ||
We can convert decimal numbers to fractions. For example, we can convert <math>2.625</math> to the improper fraction <math>\tfrac{21}{8}</math> with | We can convert decimal numbers to fractions. For example, we can convert <math>2.625</math> to the improper fraction <math>\tfrac{21}{8}</math> with | ||
< | <syntaxhighlight lang=apl> | ||
(1∧⊢,÷)2.625 | (1∧⊢,÷)2.625 | ||
21 8 | 21 8 | ||
</ | </syntaxhighlight> | ||
Alternatively, we can convert it to the mixed fraction <math>2\tfrac{5}{8}</math> with a mixed fraction: | Alternatively, we can convert it to the mixed fraction <math>2\tfrac{5}{8}</math> with a mixed fraction: | ||
< | <syntaxhighlight lang=apl> | ||
(1∧0 1∘⊤,÷)2.625 | (1∧0 1∘⊤,÷)2.625 | ||
2 5 8 | 2 5 8 | ||
</ | </syntaxhighlight> | ||
=== Is it a palindrome? === | === Is it a palindrome? === | ||
< | <syntaxhighlight lang=apl> | ||
(⌽≡⊢)'racecar' | (⌽≡⊢)'racecar' | ||
1 | 1 | ||
(⌽≡⊢)'racecat' | (⌽≡⊢)'racecat' | ||
0 | 0 | ||
</ | </syntaxhighlight> | ||
=== Split delimited text === | === Split delimited text === | ||
< | <syntaxhighlight lang=apl> | ||
','(≠⊆⊢)'comma,delimited,text' | ','(≠⊆⊢)'comma,delimited,text' | ||
┌─────┬─────────┬────┐ | ┌─────┬─────────┬────┐ | ||
| Line 168: | Line 162: | ||
│space│delimited│text│ | │space│delimited│text│ | ||
└─────┴─────────┴────┘ | └─────┴─────────┴────┘ | ||
</ | </syntaxhighlight> | ||
=== Component of a vector in the direction of another vector === | === Component of a vector in the direction of another vector === | ||
Sometimes a train can make an expression nicely resemble its equivalent definition in traditional mathematical notation. As an example, here is a program to compute the component of a vector <math>\textbf{a}</math> in the direction of another vector <math>\textbf{b}</math>: | Sometimes a train can make an expression nicely resemble its equivalent definition in traditional mathematical notation. As an example, here is a program to compute the component of a vector <math>\textbf{a}</math> in the direction of another vector <math>\textbf{b}</math>: | ||
:::<math>\textbf{a}_\textbf{b} = (\textbf{a}\cdot\hat{\textbf{b}})\hat{\textbf{b}}</math> | :::<math>\textbf{a}_\textbf{b} = (\textbf{a}\cdot\hat{\textbf{b}})\hat{\textbf{b}}</math> | ||
< | <syntaxhighlight lang=apl> | ||
Root ← *∘÷⍨ ⍝ Nth root | Root ← *∘÷⍨ ⍝ Nth root | ||
Norm ← 2 Root +.×⍨ ⍝ Magnitude (norm) of numeric vector in Euclidean space | Norm ← 2 Root +.×⍨ ⍝ Magnitude (norm) of numeric vector in Euclidean space | ||
| Line 180: | Line 174: | ||
3 5 2 InDirOf 0 0 1 ⍝ Trivial example | 3 5 2 InDirOf 0 0 1 ⍝ Trivial example | ||
0 0 2 | 0 0 2 | ||
</ | </syntaxhighlight> | ||
For a more parallel comparison of the notations, see the [[Comparison_with_traditional_mathematics#Practical_example|comparison with traditional mathematics]]. | For a more parallel comparison of the notations, see the [[Comparison_with_traditional_mathematics#Practical_example|comparison with traditional mathematics]]. | ||
===The Number of the Beast=== | ===The Number of the Beast=== | ||
The following expression for computing the [[wikipedia:666 (number)|number of the Beast]] (and of [[I.P. Sharp]]'s APL-based email system, [[666 BOX]]) nicely illustrates how to read a train. | The following expression for computing the [[wikipedia:666 (number)|number of the Beast]] (and of [[I.P. Sharp]]'s APL-based email system, [[666 BOX]]) nicely illustrates how to read a train. | ||
< | <syntaxhighlight lang=apl> | ||
((+.×⍨⊢~∘.×⍨)1↓⍳)17 ⍝ Accursed train | ((+.×⍨⊢~∘.×⍨)1↓⍳)17 ⍝ Accursed train | ||
666 | 666 | ||
</ | </syntaxhighlight> | ||
First, < | First, <syntaxhighlight lang=apl inline>((+.×⍨⊢~∘.×)1↓⍳)</syntaxhighlight> is supplied with only one argument <syntaxhighlight lang=apl inline>17</syntaxhighlight> and is thus interpreted monadically. | ||
Second, < | Second, <syntaxhighlight lang=apl inline>(+.×⍨⊢~∘.×⍨)1↓⍳</syntaxhighlight> is a 4-train: reading right-to-left, the last 3 components are interpreted as the fork <syntaxhighlight lang=apl inline>1↓⍳</syntaxhighlight> and the 4-train is interpreted as the atop <syntaxhighlight lang=apl inline>(+.×⍨⊢~∘.×⍨)(1↓⍳)</syntaxhighlight>. | ||
Similarly, < | Similarly, <syntaxhighlight lang=apl inline>(+.×⍨⊢~∘.×⍨)</syntaxhighlight> is also a 4-train and interpreted as the atop <syntaxhighlight lang=apl inline>+.×⍨(⊢~∘.×⍨)</syntaxhighlight>. | ||
Thus the accursed train is interpreted as < | Thus the accursed train is interpreted as <syntaxhighlight lang=apl inline>((+.×⍨(⊢~∘.×⍨))(1↓⍳))17</syntaxhighlight>. Having read the train, we now evaluate it monadically. | ||
< | <syntaxhighlight lang=apl> | ||
((+.×⍨(⊢~∘.×⍨))(1↓⍳))17 ⍝ Accursed train as an atop over a fork atop a fork | ((+.×⍨(⊢~∘.×⍨))(1↓⍳))17 ⍝ Accursed train as an atop over a fork atop a fork | ||
+.×⍨(⊢~∘.×⍨)1↓⍳17 ⍝ Atop evalution | +.×⍨(⊢~∘.×⍨)1↓⍳17 ⍝ Atop evalution | ||
| Line 202: | Line 196: | ||
+.×⍨2 3 5 7 11 13 17 ⍝ numbers 2 through 17 without those appearing in their multiplication table are primes | +.×⍨2 3 5 7 11 13 17 ⍝ numbers 2 through 17 without those appearing in their multiplication table are primes | ||
666 ⍝ the sum of the squares of the primes up to 17 | 666 ⍝ the sum of the squares of the primes up to 17 | ||
</ | </syntaxhighlight> | ||
Note that < | Note that <syntaxhighlight lang=apl inline>((⊢~∘.×⍨)1↓⍳)</syntaxhighlight> is a train computing primes up to the given input. | ||
A more satisfying variation of the accursed train is the following. | A more satisfying variation of the accursed train is the following. | ||
< | <syntaxhighlight lang=apl> | ||
(⍎⊢,⍕∘≢)'((+.×⍨⊢~∘.×⍨)1↓⍳)' ⍝ Accursed train 2.0 | (⍎⊢,⍕∘≢)'((+.×⍨⊢~∘.×⍨)1↓⍳)' ⍝ Accursed train 2.0 | ||
⍎(⊢,⍕∘≢)'((+.×⍨⊢~∘.×⍨)1↓⍳)' ⍝ 4-train intepreted as an atop | ⍎(⊢,⍕∘≢)'((+.×⍨⊢~∘.×⍨)1↓⍳)' ⍝ 4-train intepreted as an atop | ||
| Line 213: | Line 207: | ||
⍎'((+.×⍨⊢~∘.×⍨)1↓⍳)17' ⍝ , evaluation | ⍎'((+.×⍨⊢~∘.×⍨)1↓⍳)17' ⍝ , evaluation | ||
666 ⍝ ⍎ executes original Accursed train | 666 ⍝ ⍎ executes original Accursed train | ||
</ | </syntaxhighlight> | ||
== External links == | == External links == | ||
| Line 226: | Line 216: | ||
* [[Documentation_suites#Dyalog_APL|Dyalog documentation]]: [https://help.dyalog.com/16.0/Content/RelNotes14.0/Function%20Trains.htm version 14.0 release notes] | * [[Documentation_suites#Dyalog_APL|Dyalog documentation]]: [https://help.dyalog.com/16.0/Content/RelNotes14.0/Function%20Trains.htm version 14.0 release notes] | ||
* [[Dfns workspace]]: [https://dfns.dyalog.com/n_tacit.htm Translation of <nowiki>[dfns]</nowiki> into tacit form] | * [[Dfns workspace]]: [https://dfns.dyalog.com/n_tacit.htm Translation of <nowiki>[dfns]</nowiki> into tacit form] | ||
* [[Dfns workspace]]: [https://dfns.dyalog.com/n_dft.htm Display of function tree] | |||
* [[Dfns workspace]]: [https://dfns.dyalog.com/n_fork.htm Simulation of fork syntax] | |||
* [[APL Cultivation]]: [https://chat.stackexchange.com/rooms/52405/conversation/lesson-23-transcribing-to-and-reading-trains Transcribing to and reading trains] | * [[APL Cultivation]]: [https://chat.stackexchange.com/rooms/52405/conversation/lesson-23-transcribing-to-and-reading-trains Transcribing to and reading trains] | ||
* gitonthescene: [https://gist.github.com/gitonthescene/666c77ee3ed0ae0a79cf8e057584b7fd Forks: Spoon fed] | * gitonthescene: [https://gist.github.com/gitonthescene/666c77ee3ed0ae0a79cf8e057584b7fd Forks: Spoon fed] | ||
| Line 237: | Line 229: | ||
* [[Dyalog '13]]: [https://www.youtube.com/watch?v=7-93GzDqC08 Train Spotting in Version 14.0] | * [[Dyalog '13]]: [https://www.youtube.com/watch?v=7-93GzDqC08 Train Spotting in Version 14.0] | ||
</div> | </div> | ||
== References == | == References == | ||
Latest revision as of 21:28, 6 March 2024
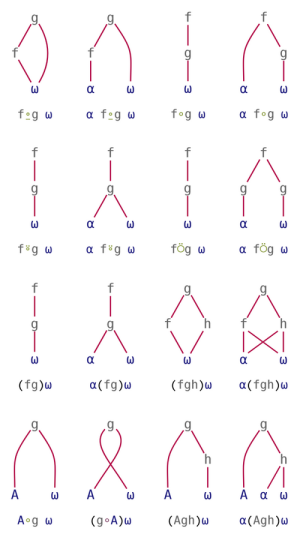
Tacit programming, also called point-free style, refers to usage of tacit functions that are defined in terms of implicit arguments. This is in contrast to the explicit use of arguments in dfns (⍺ ⍵) and tradfns (which have named arguments). Some APL dialects allow to combine functions into trains following a small set of rules. This allows creating complex derived functions without specifying any arguments explicitly.
Dialects which implement trains include Dyalog APL, dzaima/APL, ngn/apl and NARS2000.
Primitives
All primitive functions are tacit. Some APLs allow primitive functions to be named.
plus ← +
times ← ×
6 times 3 plus 5
48
Derived functions
Functions derived from a monadic operator and an operand, or from a dyadic operator and two operands are tacit functions:
Sum ← +/
Sum ⍳10
55
Dot ← +.×
3 1 4 Dot 2 7 1
17
Derived operators
A dyadic operator with its right operand forms a tacit monadic operator:
1(+⍣2)10
12
Twice ← ⍣2
1 +Twice 10
12
Trains
A train is a series of functions in isolation. An isolated function is either surrounded by parentheses or named.
These rules are used for 3-trains, called forks:
(f g h) ⍵ |
( f ⍵) g ( h ⍵) | |
⍺ (f g h) ⍵ |
(⍺ f ⍵) g (⍺ h ⍵) |
The left tine of a fork can be an array:
(A g h) ⍵ |
A g ( h ⍵) | |
⍺ (A g h) ⍵ |
A g (⍺ h ⍵) |
In APL (but not J), these rules are used for 2-trains, called atops:
(g h) ⍵ |
g ( h ⍵) | |
⍺ (g h) ⍵ |
g (⍺ h ⍵) |
Any train can be expressed in terms of function composition — except dyadic forks. Some common patterns are:
(f g h) ⍵ |
g⍨∘f⍨∘h⍨ ⍵ | |
(f g f) ⍵ |
g⍥f⍨ ⍵ | |
(⊢ g f) ⍵ |
g∘f⍨ ⍵ |
Debugging
In Dyalog APL, analysis of trains is assisted by a user command ]Boxing on. This is achieved by executing the command ]Boxing on and then entering a train without any parameters. A structure of the train will be displayed.
For example, the "accursed train" from the section below can be analysed like this:
]Boxing on
Was OFF
((+.×⍨⊢~∘.×⍨)1↓⍳) ⍝ the train to be analysed
┌───────────────────────────────┬───────┐
│┌───────────┬─────────────────┐│┌─┬─┬─┐│
││┌───────┬─┐│┌─┬─┬───────────┐│││1│↓│⍳││
│││┌─┬─┬─┐│⍨│││⊢│~│┌───────┬─┐│││└─┴─┴─┘│
││││+│.│×││ │││ │ ││┌─┬─┬─┐│⍨││││ │
│││└─┴─┴─┘│ │││ │ │││∘│.│×││ ││││ │
││└───────┴─┘││ │ ││└─┴─┴─┘│ ││││ │
││ ││ │ │└───────┴─┘│││ │
││ │└─┴─┴───────────┘││ │
│└───────────┴─────────────────┘│ │
└───────────────────────────────┴───────┘
Alternatively, a train can be represented in form of a tree:
]Boxing on -trains=tree
Was ON -trains=box
((+.×⍨⊢~∘.×⍨)1↓⍳) ⍝ the train to be analysed
┌───┴───┐
┌─┴─┐ ┌─┼─┐
⍨ ┌─┼─┐ 1 ↓ ⍳
┌─┘ ⊢ ~ ⍨
. ┌─┘
┌┴┐ .
+ × ┌┴┐
∘ ×
Or fully parenthesised:
]Boxing on -trains=parens
Was OFF -trains=box
((+.×⍨⊢~∘.×⍨)1↓⍳) ⍝ the train to be analysed
(((+.×)⍨)(⊢~((∘.×)⍨)))(1↓⍳)
Conversion to dfns
It can help understanding to convert a tacit function to a dfn. For many tacit functions, it is not immediately clear if the intention of the function is to be used monadically or dyadically, or even both. Such knowledge can be conveyed by comments, but sometimes it is possible to spot patterns that are exclusively monadic or dyadic: A function with a bound argument (for example +∘1) can indicate a monadic function, and in some contexts, =, which can only be used dyadically, would indicate a dyadic function. The website tacit.help provides automated translation of most tacit functions, into both monadic and dyadic, fully parenthesised dfns.
Examples
One of the major benefits of tacit programming is the ability to convey a short, well-defined idea as an isolated expression. This aids both human readability (semantic density) and the computer's ability to interpret code, potentially executing special code for particular idioms.
Plus and minus
(+,-) 2 ⍝ ±2
2 ¯2
5 (+,-) 2 ⍝ 5±2
7 3
Arithmetic mean
(+⌿÷≢) ⍳10 ⍝ Mean of the first ten integers
5.5
(+⌿÷≢) 5 4⍴⍳4 ⍝ Mean of columns in a matrix
1 2 3 4
Fractions
We can convert decimal numbers to fractions. For example, we can convert to the improper fraction with
(1∧⊢,÷)2.625 21 8
Alternatively, we can convert it to the mixed fraction with a mixed fraction:
(1∧0 1∘⊤,÷)2.625 2 5 8
Is it a palindrome?
(⌽≡⊢)'racecar'
1
(⌽≡⊢)'racecat'
0
Split delimited text
','(≠⊆⊢)'comma,delimited,text'
┌─────┬─────────┬────┐
│comma│delimited│text│
└─────┴─────────┴────┘
' '(≠⊆⊢)'space delimited text'
┌─────┬─────────┬────┐
│space│delimited│text│
└─────┴─────────┴────┘
Component of a vector in the direction of another vector
Sometimes a train can make an expression nicely resemble its equivalent definition in traditional mathematical notation. As an example, here is a program to compute the component of a vector in the direction of another vector :
Root ← *∘÷⍨ ⍝ Nth root
Norm ← 2 Root +.×⍨ ⍝ Magnitude (norm) of numeric vector in Euclidean space
Unit ← ⊢÷Norm ⍝ Unit vector in direction of vector ⍵
InDirOf ← (⊢×+.×)∘Unit ⍝ Component of vector ⍺ in direction of vector ⍵
3 5 2 InDirOf 0 0 1 ⍝ Trivial example
0 0 2
For a more parallel comparison of the notations, see the comparison with traditional mathematics.
The Number of the Beast
The following expression for computing the number of the Beast (and of I.P. Sharp's APL-based email system, 666 BOX) nicely illustrates how to read a train.
((+.×⍨⊢~∘.×⍨)1↓⍳)17 ⍝ Accursed train 666
First, ((+.×⍨⊢~∘.×)1↓⍳) is supplied with only one argument 17 and is thus interpreted monadically.
Second, (+.×⍨⊢~∘.×⍨)1↓⍳ is a 4-train: reading right-to-left, the last 3 components are interpreted as the fork 1↓⍳ and the 4-train is interpreted as the atop (+.×⍨⊢~∘.×⍨)(1↓⍳).
Similarly, (+.×⍨⊢~∘.×⍨) is also a 4-train and interpreted as the atop +.×⍨(⊢~∘.×⍨).
Thus the accursed train is interpreted as ((+.×⍨(⊢~∘.×⍨))(1↓⍳))17. Having read the train, we now evaluate it monadically.
((+.×⍨(⊢~∘.×⍨))(1↓⍳))17 ⍝ Accursed train as an atop over a fork atop a fork
+.×⍨(⊢~∘.×⍨)1↓⍳17 ⍝ Atop evalution
+.×⍨(⊢1↓⍳17)~∘.×⍨1↓⍳17 ⍝ Fork evalution
+.×⍨(1↓⍳17)~∘.×⍨1↓⍳17 ⍝ ⊢ evaluation
+.×⍨2 3 5 7 11 13 17 ⍝ numbers 2 through 17 without those appearing in their multiplication table are primes
666 ⍝ the sum of the squares of the primes up to 17
Note that ((⊢~∘.×⍨)1↓⍳) is a train computing primes up to the given input.
A more satisfying variation of the accursed train is the following.
(⍎⊢,⍕∘≢)'((+.×⍨⊢~∘.×⍨)1↓⍳)' ⍝ Accursed train 2.0
⍎(⊢,⍕∘≢)'((+.×⍨⊢~∘.×⍨)1↓⍳)' ⍝ 4-train intepreted as an atop
⍎(⊢'((+.×⍨⊢~∘.×⍨)1↓⍳)'),⍕∘≢'((+.×⍨⊢~∘.×⍨)1↓⍳)' ⍝ fork evaluation
⍎'((+.×⍨⊢~∘.×⍨)1↓⍳)','17' ⍝ ⊢ evaluation and ⍕∘≢ evaluation
⍎'((+.×⍨⊢~∘.×⍨)1↓⍳)17' ⍝ , evaluation
666 ⍝ ⍎ executes original Accursed train
External links
Tutorials
In text form
- Learning APL: Trainspotting
- Dyalog documentation: version 14.0 release notes
- Dfns workspace: Translation of [dfns] into tacit form
- Dfns workspace: Display of function tree
- Dfns workspace: Simulation of fork syntax
- APL Cultivation: Transcribing to and reading trains
- gitonthescene: Forks: Spoon fed
- gitonthescene: Training day
Videos
References






